初中数学浙教版七年级上册第六章 图形的初步知识 单元检测(基础篇)
试卷更新日期:2020-11-02 类型:单元试卷
一、单选题
-
1. 图绕虚线旋转得到的实物图是( )
 A、
A、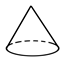 B、
B、 C、
C、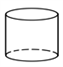 D、
D、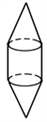 2. 下列四个生产生活现象,可以用“两点之间线段最短”来解释的现象有( )A、用两个钉子将木条固定在墙上 B、打靶时,眼睛要与准星、靶心在同一条直线上 C、架设A,B两地的电线时,总是尽可能沿着线段AB架设 D、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线3. 下列说法中,正确的是( )A、一根绳子,不用任何工具,可以找到它的中点 B、一条直线就是一个平角 C、若 ,则点B是线段AC的中点 D、两个锐角的度数和一定大于4. 下列四个图形中, 能用∠1、∠AOB、∠O三种方法表示同一个角的( )A、
2. 下列四个生产生活现象,可以用“两点之间线段最短”来解释的现象有( )A、用两个钉子将木条固定在墙上 B、打靶时,眼睛要与准星、靶心在同一条直线上 C、架设A,B两地的电线时,总是尽可能沿着线段AB架设 D、植树时,只要定出两棵树的位置,就能确定同一行树所在的直线3. 下列说法中,正确的是( )A、一根绳子,不用任何工具,可以找到它的中点 B、一条直线就是一个平角 C、若 ,则点B是线段AC的中点 D、两个锐角的度数和一定大于4. 下列四个图形中, 能用∠1、∠AOB、∠O三种方法表示同一个角的( )A、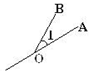 B、
B、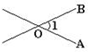 C、
C、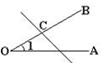 D、
D、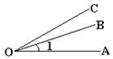 5.
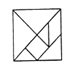
5.下列拼图中,不是由原图这副七巧板拼成的是( )
 A、
A、 B、
B、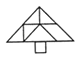 C、
C、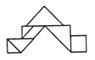 D、
D、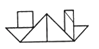 6. 如图所示,从A村出发经C村到B村,最近的路程是( )
6. 如图所示,从A村出发经C村到B村,最近的路程是( )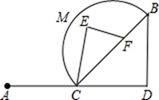 A、A-C-D-B B、A-C-E-F-B C、A-C-F-B D、A-C-M-B7. 如果点B在线段AC上,那么下列表达式中:①AB=
A、A-C-D-B B、A-C-E-F-B C、A-C-F-B D、A-C-M-B7. 如果点B在线段AC上,那么下列表达式中:①AB= AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有( )
AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有( ) A.1个 B.2个 C.3个 D.4个
A、1个 B、2个 C、3个 D、4个8. 如图.∠AOB=∠COD,则( )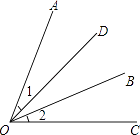 A、∠1>∠2 B、∠1=∠2 C、∠1<∠2 D、∠1与∠2的大小无法比较9. ∠AOB的大小可由量角器测得(如图所示),则180°-∠AOB的大小为( )
A、∠1>∠2 B、∠1=∠2 C、∠1<∠2 D、∠1与∠2的大小无法比较9. ∠AOB的大小可由量角器测得(如图所示),则180°-∠AOB的大小为( )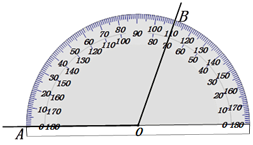 A、0° B、70° C、110° D、180°10. 如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( )A、50° B、70° C、130° D、160°
A、0° B、70° C、110° D、180°10. 如果一个角的度数比它的补角的度数2倍多30°,那么这个角的度数是( )A、50° B、70° C、130° D、160°二、填空题
-
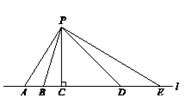
11. 已知∠α=25°15′,∠β=25.15°,则∠α∠β(填“>”,“<”或“=”).12. 如图,要从村庄P修一条连接公路 的最短的小道,应选择沿线段修建,理由是 .
 13. 如图,已知直线AB,CD,MN相交于O,若∠1=21°,∠2=47°,则∠3的度数为
13. 如图,已知直线AB,CD,MN相交于O,若∠1=21°,∠2=47°,则∠3的度数为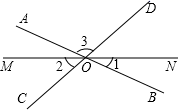 14. 建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后就可以在两根木桩间拉一根直的参照线,其理由是 .15. 如图,C是线段AB上的一点,M是线段AC的中点,若AB=10cm , BC=2cm , 则AM的长为 .
14. 建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后就可以在两根木桩间拉一根直的参照线,其理由是 .15. 如图,C是线段AB上的一点,M是线段AC的中点,若AB=10cm , BC=2cm , 则AM的长为 . 16. 如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB= .
16. 如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB= .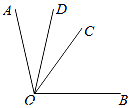
三、解答题
-
17. 写出下图中各个几何体的名称,并按锥体和柱体把它们分类.
 18. 如图,在平面内有A,B,C三点.
18. 如图,在平面内有A,B,C三点.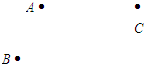 (1)、①画直线AC,线段BC,射线AB;
(1)、①画直线AC,线段BC,射线AB;②在线段BC上任取一点 不同于B, ,连接线段AD;
(2)、数数看,此时图中线段的条数.19. 如图,点C是 的边OB上的一点,按下列要求画图并回答问题. (1)、①过点C画OA的垂线,交OA与点D;
(1)、①过点C画OA的垂线,交OA与点D;②过点C画OB的垂线,交OA与点E;
(2)、比较线段CD,CE,OE的大小,并用“<”连接.20. 如图,C 为线段 AB 的中点,点 D 在线段 CB 上.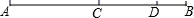 (1)、图中共有几条线段;(2)、图中AD=AC+CD,BC=AB-AC,类似地,请你再写出两个有关线段的和与差的关系式:①;②;21. 如图,已知 , , .
(1)、图中共有几条线段;(2)、图中AD=AC+CD,BC=AB-AC,类似地,请你再写出两个有关线段的和与差的关系式:①;②;21. 如图,已知 , , .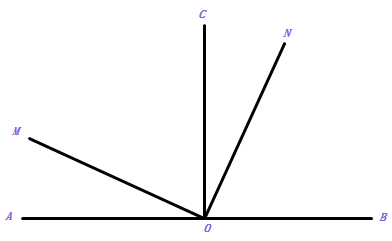 (1)、指出图中所有互为补角的角.(2)、求 的度数.22. 已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)、指出图中所有互为补角的角.(2)、求 的度数.22. 已知:直线AB与直线CD交于点O,过点O作OE⊥AB.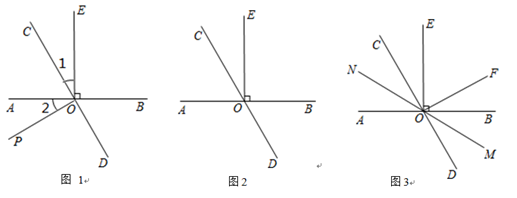 (1)、如图1,OP为∠AOD内的一条射线,若∠1=∠2,求证:OP⊥CD;(2)、如图2,若∠BOC=2∠AOC,求∠COE的度数;(3)、如图3.在(2)的条件下,过点O作OF⊥CD,经过点O画直线MN,若射线OM平分∠BOD,请直接写出图中与2∠EOF度数相等的角.23. 在三角形AOB和三角形COD中,∠AOB=∠COD ,
(1)、如图1,OP为∠AOD内的一条射线,若∠1=∠2,求证:OP⊥CD;(2)、如图2,若∠BOC=2∠AOC,求∠COE的度数;(3)、如图3.在(2)的条件下,过点O作OF⊥CD,经过点O画直线MN,若射线OM平分∠BOD,请直接写出图中与2∠EOF度数相等的角.23. 在三角形AOB和三角形COD中,∠AOB=∠COD ,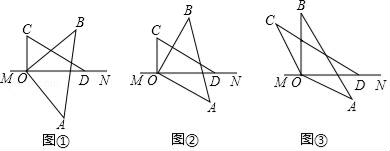 (1)、已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.(2)、已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.(3)、当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD .24. 点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC.
(1)、已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.(2)、已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.(3)、当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD .24. 点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC. (1)、①如图1,若∠DOE=25°,求∠AOC 的度数;
(1)、①如图1,若∠DOE=25°,求∠AOC 的度数;②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)、将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置.探究∠DOE 与∠AOC 的度数之间的关系,写出你的结论,并说明理由.