安徽省池州市东至县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、7 cm、5 cm、10 cm B、4 cm、3 cm、7 cm C、5 cm、10 cm、4 cm D、2 cm、3 cm、1cm2. 下列命题与其逆命题都是真命题的是( )A、全等三角形对应角相等 B、对顶角相等 C、角平分线上的点到角的两边的距离相等 D、若a2>b2,则a>b3. 如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1 , 则a+b的值为( )
 A、2 B、3 C、4 D、54. 如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )
A、2 B、3 C、4 D、54. 如图,OP是∠AOB的平分线,点P到OA的距离为3,点N是OB上的任意一点,则线段PN的取值范围为( )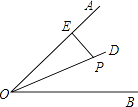 A、PN<3 B、PN>3 C、PN≥3 D、PN≤35. 如图,在△ABC中,AB=BC , 顶点B在y轴上,顶点C的坐标为(2,0),若一次函数y=kx+2的图象经过点A , 则k的值为( )
A、PN<3 B、PN>3 C、PN≥3 D、PN≤35. 如图,在△ABC中,AB=BC , 顶点B在y轴上,顶点C的坐标为(2,0),若一次函数y=kx+2的图象经过点A , 则k的值为( ) A、 B、- C、1 D、-16. 如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD , 有下列四个结论:①∠PBC=15°,②AD∥BC , ③PC⊥AB , ④四边形ABCD是轴对称图形,其中正确的个数为( )
A、 B、- C、1 D、-16. 如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD , 有下列四个结论:①∠PBC=15°,②AD∥BC , ③PC⊥AB , ④四边形ABCD是轴对称图形,其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个7. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
A、1个 B、2个 C、3个 D、4个7. 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( ) A、
A、 B、
B、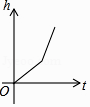 C、
C、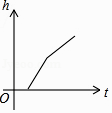 D、
D、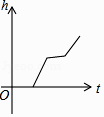 8. 如图,在△ABC中,点D,E,F分别在三边上,点E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是( )
8. 如图,在△ABC中,点D,E,F分别在三边上,点E是AC的中点,AD,BE,CF交于一点G,BD=2DC,S△BGD=8,S△AGE=3,则△ABC的面积是( )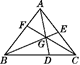 A、25 B、30 C、35 D、409. 如图,∠ABD、∠ACD的角平分线交于点P , 若∠A=60°,∠D=20°,则∠P的度数为( )
A、25 B、30 C、35 D、409. 如图,∠ABD、∠ACD的角平分线交于点P , 若∠A=60°,∠D=20°,则∠P的度数为( ) A、15° B、20° C、25° D、30°10. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )
A、15° B、20° C、25° D、30°10. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )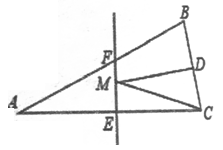 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
11. 函数 的自变量 的取值范围是12. 已知 与 成正比例,且当 时, 则 与 的函数关系式为13. 如图,在 若中, 是 边上的高, 是 平分线.若 则 =
 14. 把一个等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(﹣5,5),则点C的坐标为.
14. 把一个等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(﹣5,5),则点C的坐标为. 15. 一次函数 ,当 时, ,那么不等式 的解集为.16. 如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
15. 一次函数 ,当 时, ,那么不等式 的解集为.16. 如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .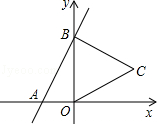 17. 新定义:[a,b]为一次函数 (a≠0,a、b为实数)的“关联数”.若“关联数”为[3,m-2] 的一次函数是正比例函数,则点(1-m,1+m)在第象限.18. 如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为.
17. 新定义:[a,b]为一次函数 (a≠0,a、b为实数)的“关联数”.若“关联数”为[3,m-2] 的一次函数是正比例函数,则点(1-m,1+m)在第象限.18. 如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为.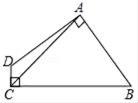
三、解答题
-
19. 在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).(1)、当﹣2<x≤3时,求y的取值范围;(2)、已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.20. 当在边长为1的正方形网格中建立如图所示的平面直角坐标系,点 、点 的坐标分别为 ,
 (1)、画出 时关于 轴对称图形;(2)、在平面直角坐标系内找一点 求(不与点 重合),使 与 全等,求请直接写出所有可能的点 的坐标.21.
(1)、画出 时关于 轴对称图形;(2)、在平面直角坐标系内找一点 求(不与点 重合),使 与 全等,求请直接写出所有可能的点 的坐标.21.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.

求证:
(1)、△AEF≌△CEB;(2)、AF=2CD.22. 如图在中 , , , 是 的平分线,交 于点 , 是 的中点,连接 并延长交 的延长线于点 ,连接 .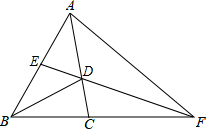
求证:
(1)、 ;(2)、 为等腰三角形23. 如图,直线 角形与两坐标轴分别交于 ,直线 与 轴交于点 与直线 交于点 面积为 . (1)、求 的值(2)、直接写出不等式 的解集;(3)、点 在 上,如果 的面积为4,点 的坐标.24. “六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
(1)、求 的值(2)、直接写出不等式 的解集;(3)、点 在 上,如果 的面积为4,点 的坐标.24. “六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表: (1)、小张如何进货,使进货款恰好为1300元?(2)、要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.25. 在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α.
(1)、小张如何进货,使进货款恰好为1300元?(2)、要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.25. 在△ABC和△DCE中,CA=CB,CD=CE,∠CAB= ∠CED=α. (1)、如图1,将AD、EB延长,延长线相交于点0.
(1)、如图1,将AD、EB延长,延长线相交于点0.①求证:BE= AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)、如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N.求证:N是BD的中点.注:第(2)问的解答过程无需注明理由.