安徽省安庆市太湖县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、2. 已知 是整数,点 在第四象限,则a的值是( )A、-1 B、0 C、1 D、23. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知三角形两边的长分别是5和11,则此三角形第三边的长可能是( )A、5 B、15 C、3 D、165. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点
4. 已知三角形两边的长分别是5和11,则此三角形第三边的长可能是( )A、5 B、15 C、3 D、165. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点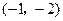 .“馬”位于点
.“馬”位于点  ,则“兵”位于点( )
,则“兵”位于点( ) 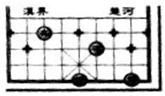 A、 B、 C、 D、6. 如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )
A、 B、 C、 D、6. 如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )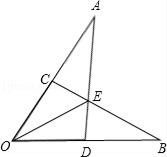 A、2对 B、3对 C、4对 D、5对7. 一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是( )
A、2对 B、3对 C、4对 D、5对7. 一根直尺EF压在三角板30°的角∠BAC上,与两边AC,AB交于M、N.那么∠CME+∠BNF是( )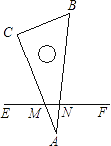 A、150° B、180° C、135° D、不能确定8. 一次函数y=-3x-2的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,平面直角坐标系中,在边长为1的正方形 的边上有—动点 沿正方形运动一周, 则 的纵坐标 与点 走过的路程 之间的函数关系用图象表示大致是( )
A、150° B、180° C、135° D、不能确定8. 一次函数y=-3x-2的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,平面直角坐标系中,在边长为1的正方形 的边上有—动点 沿正方形运动一周, 则 的纵坐标 与点 走过的路程 之间的函数关系用图象表示大致是( ) A、
A、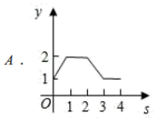 B、
B、 C、
C、 D、
D、 10. 直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )A、10000 B、10050 C、10100 D、10150
10. 直线y=kx+k(k为正整数)与坐标轴所构成的直角三角形的面积为Sk , 当k分别为1,2,3,…,199,200时,则S1+S2+S3+…+S199+S200=( )A、10000 B、10050 C、10100 D、10150二、填空题
-
11. 命题“全等三角形的面积相等”的逆命题是命题.(填入“真”或“假”)12. 写一个函数图象交 轴于点 ,且 随 的增大而增大的一次函数关系式 .13. 点 关于 轴的对称点 的坐标 .14. 有一张三角形纸片ABC , ∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两张纸片均为等腰三角形,则∠C的度数可以是 .
三、解答题
-
15. 在平面直角坐标系中的位置如图所示.
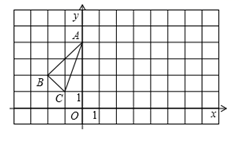 (1)、作出 关于 轴对称的 ,并写出 各顶点的坐标;(2)、将 向右平移6个单位,作出平移后的 并写出 各顶点的坐标;(3)、观察 和 ,它们是否关于某直线对称?若是,请用粗线条画出对称轴.16. 如图, 、 分别垂直于 ,点 、 是垂足,且 , ,求证: 是直角三角形.
(1)、作出 关于 轴对称的 ,并写出 各顶点的坐标;(2)、将 向右平移6个单位,作出平移后的 并写出 各顶点的坐标;(3)、观察 和 ,它们是否关于某直线对称?若是,请用粗线条画出对称轴.16. 如图, 、 分别垂直于 ,点 、 是垂足,且 , ,求证: 是直角三角形.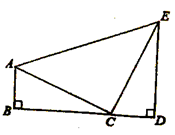 17. 如图直线 对应的函数表达式为 ,直线 与 轴交于点 .直线 : 与 轴交于点 ,且经过点 ,直线 , 交于点 .
17. 如图直线 对应的函数表达式为 ,直线 与 轴交于点 .直线 : 与 轴交于点 ,且经过点 ,直线 , 交于点 . (1)、求点 ,点 的坐标;(2)、求直线 对应的函数表达式;(3)、求 的面积;(4)、利用函数图象写出关于 , 的二元一次方程组 的解.18. 已知 与 成正比例, , 为常数(1)、试说明: 是 的一次函数;(2)、若 时, ; 时, ,求函数关系式;(3)、将(2)中所得的函数图象平移,使它过点 ,求平移后的直线的解析式.19. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中 , , , , 、 、 在同一条直线上,连结 .
(1)、求点 ,点 的坐标;(2)、求直线 对应的函数表达式;(3)、求 的面积;(4)、利用函数图象写出关于 , 的二元一次方程组 的解.18. 已知 与 成正比例, , 为常数(1)、试说明: 是 的一次函数;(2)、若 时, ; 时, ,求函数关系式;(3)、将(2)中所得的函数图象平移,使它过点 ,求平移后的直线的解析式.19. 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中 , , , , 、 、 在同一条直线上,连结 . (1)、请在图2中找出与 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)、证明: .20. 某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.(1)、求A、B两种奖品的单价各是多少元?(2)、学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.21. 探索与证明:
(1)、请在图2中找出与 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)、证明: .20. 某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.(1)、求A、B两种奖品的单价各是多少元?(2)、学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.21. 探索与证明: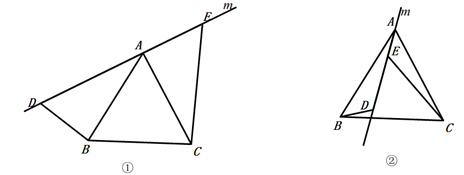 (1)、如图①,直线 经过正三角形 的顶点 ,在直线 上取点 , ,使得 , .通过观察或测量,猜想线段 , 与 之间满足的数量关系,并予以证明;(2)、将(1)中的直线 绕着点 逆时针方向旋转一个角度到如图②的位置, , .通过观察或测量,猜想线段 , 与 之间满足的数量关系,并予以证明.
(1)、如图①,直线 经过正三角形 的顶点 ,在直线 上取点 , ,使得 , .通过观察或测量,猜想线段 , 与 之间满足的数量关系,并予以证明;(2)、将(1)中的直线 绕着点 逆时针方向旋转一个角度到如图②的位置, , .通过观察或测量,猜想线段 , 与 之间满足的数量关系,并予以证明.