广西来宾市合山市2021届九年级上学期数学第一次月考试卷
试卷更新日期:2020-11-02 类型:月考试卷
一、选择题(共12小题,每小题3分,共36分。在每小题给出的四个选项中只有-项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑。)
-
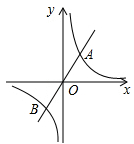
1. 下列关系式中,y是x的反比例函数的是( )A、y=5x B、 =3 C、y= D、y=x2-32. 若反比例函数y= 的图象在第二,四象限,则m的值是( )A、m> B、m< C、m>2 D、m<23. 如图,双曲线y= 与直线y=mx相交于A、B两点,B点坐标为(-2,-3),则A点坐标为( )
 A、(-2,-3) B、(2,3) C、(-2,3) D、(2,-3)4. 对于反比例函数y= 的图象的对称性叙述错误的是( )A、关于原点中心对称 B、关于直线y=x对称 C、关于直线y=-x对称 D、关于x轴对称5. 反比例函数y= 图象如图所示,下列说法正确的是( )
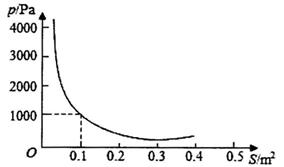
A、(-2,-3) B、(2,3) C、(-2,3) D、(2,-3)4. 对于反比例函数y= 的图象的对称性叙述错误的是( )A、关于原点中心对称 B、关于直线y=x对称 C、关于直线y=-x对称 D、关于x轴对称5. 反比例函数y= 图象如图所示,下列说法正确的是( )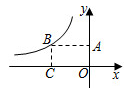 A、k>0 B、y随x的增大而减小. C、若矩形OABC面积为2,则k=-2 D、若图象上点B的坐标是(-2,1),则当x<-2时,y的取值范围是y<16. 若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y37. 已知y是关于x的反比例函数,且当x= 时,y=2。则y关于x的函数表达式为( )A、y=-x B、y= C、y= x D、y=8. 对于方程2x2=3x,下列说法正确的是( )A、一次项系数为3 B、一次项系数为-3 C、常数项是3 D、方程的解为x=39. 若x=-1是关于x的一元二次方程ax2+bx-1=0的一个根,则2020+2a-2b的值为( )A、2018 B、2020 C、2022 D、202410. 一元二次方程y2+y- =0配方后可化为( )A、(y+ )2=1 B、(y- )2=1 C、(y+ )2= D、(y- )2=11. 若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为( )A、16 B、24 C、16或24 D、4812. 当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P= (S≠0),这个反比例函数的图象大致是( )A、
A、k>0 B、y随x的增大而减小. C、若矩形OABC面积为2,则k=-2 D、若图象上点B的坐标是(-2,1),则当x<-2时,y的取值范围是y<16. 若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y= 的图象上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y2<y3<y1 C、y3<y2<y1 D、y2<y1<y37. 已知y是关于x的反比例函数,且当x= 时,y=2。则y关于x的函数表达式为( )A、y=-x B、y= C、y= x D、y=8. 对于方程2x2=3x,下列说法正确的是( )A、一次项系数为3 B、一次项系数为-3 C、常数项是3 D、方程的解为x=39. 若x=-1是关于x的一元二次方程ax2+bx-1=0的一个根,则2020+2a-2b的值为( )A、2018 B、2020 C、2022 D、202410. 一元二次方程y2+y- =0配方后可化为( )A、(y+ )2=1 B、(y- )2=1 C、(y+ )2= D、(y- )2=11. 若菱形ABCD的一条对角线长为8,边CD的长是方程x2-10x+24=0的一个根,则该菱形ABCD的周长为( )A、16 B、24 C、16或24 D、4812. 当压力F(N)一定时,物体所受的压强p(Pa)与受力面积S(m2)的函数关系式为P= (S≠0),这个反比例函数的图象大致是( )A、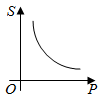 B、
B、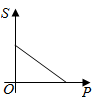 C、
C、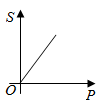 D、
D、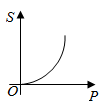
二、填空题(每小题3分,满分18分)
-
13. 若关于x的方程(a-1)xa2+1-7=0是一元二次方程,则a=。14. 方程(x-1)2=20202的根是。15. 反比例函数y= (x<0)的图象如图所示,则m的取值范围为 。
 16. 如图,B(2,-2),C(3,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为。
16. 如图,B(2,-2),C(3,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为。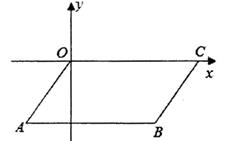 17. 如图,经过原点的直线与反比例函数y= (k>0)相交于A,B两点,BC⊥x轴。若△ABC的面积为4,则k的值为。
17. 如图,经过原点的直线与反比例函数y= (k>0)相交于A,B两点,BC⊥x轴。若△ABC的面积为4,则k的值为。 18. 反比例函数y= (x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=-x对称;④若点(-2,3)在该反比例函数图象上,则点(-1,6)也在该函数的图象上.其中正确结论的个数有 个。
18. 反比例函数y= (x<0)的图象如图所示,下列关于该函数图象的四个结论:①k>0;②当x<0时,y随x的增大而增大;③该函数图象关于直线y=-x对称;④若点(-2,3)在该反比例函数图象上,则点(-1,6)也在该函数的图象上.其中正确结论的个数有 个。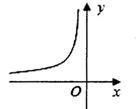
三、解答题(共66分)
-
19. 解一元二次方程:(1)、x2-9=0;(2)、x2-2x-3=020. 已知y是x的反比例函数,且x=3时,y=8。(1)、写出y与x之间的函数关系式;(2)、如果自变量x的取值范围为3≤x≤4.求y的取值范围。21. 已知二次三项式4x2+8x+8,圆圆同学对其进行变形如下:
4x2+8x+8=x2+2x+2=(x+1)2+1,所以圆圆得到结论:当x=-1时,这个二次三项式有最小值为1。
圆圆的解答正确吗?如果不正确,写出正确的解答。
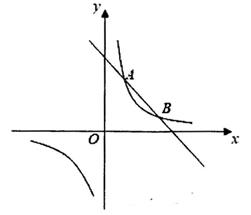
22. 已知,反比例函数y= (k是常数,且k≠0)的图象经过点A(b,3)。(1)、若b=4,求y关于x的函数;(2)、若点B(3b,3b)也在该反比例函数图象上,求b的值。23. 如图,一次函数y1=- x+3与反比例函数y2= 的图象交于A、B两点,A点的横坐标为3。 (1)、求反比例函数的解析式;(2)、结合图象,直接写出y1<y2时,x的取值范围。24. 已知x=2是关于x的方程x2-(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰三角形ABC的两条边长,(1)、求m的值;(2)、求△ABC的周长。
(1)、求反比例函数的解析式;(2)、结合图象,直接写出y1<y2时,x的取值范围。24. 已知x=2是关于x的方程x2-(m+4)x+4m=0的一个实数根,并且这个方程的两个实数根恰好是等腰三角形ABC的两条边长,(1)、求m的值;(2)、求△ABC的周长。