安徽省铜陵市枞阳县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知关于 的一元二次方程 有一个根是-2,那么 的值是( )A、-2 B、-1 C、2 D、103. 二次函数y=x2+2x+2与坐标轴的交点个数是( )A、0个 B、1个 C、2个 D、3个4. 从1、2、3、4四个数中随机选取两个不同的数,分别记为 , ,则满足 的概率为( )A、 B、 C、 D、5. 设 , , 是抛物线 上的三点,则 的大小关系为( )A、 B、 C、 D、6. 某市为了改善城市容貌,绿化环境,计划过两年时间,绿地面积增加44%,这两年平均每年绿地面积的增长率是 ( )A、19% B、20% C、21% D、22%7. 如图,⊙ 是 的外接圆, ,则 的度数为( )
2. 已知关于 的一元二次方程 有一个根是-2,那么 的值是( )A、-2 B、-1 C、2 D、103. 二次函数y=x2+2x+2与坐标轴的交点个数是( )A、0个 B、1个 C、2个 D、3个4. 从1、2、3、4四个数中随机选取两个不同的数,分别记为 , ,则满足 的概率为( )A、 B、 C、 D、5. 设 , , 是抛物线 上的三点,则 的大小关系为( )A、 B、 C、 D、6. 某市为了改善城市容貌,绿化环境,计划过两年时间,绿地面积增加44%,这两年平均每年绿地面积的增长率是 ( )A、19% B、20% C、21% D、22%7. 如图,⊙ 是 的外接圆, ,则 的度数为( ) A、60° B、65° C、70° D、75°8. 如图,若一次函数y=ax+b的图象经过二、三、四象限,则二次函数y=ax2+bx的图象可能是( )A、
A、60° B、65° C、70° D、75°8. 如图,若一次函数y=ax+b的图象经过二、三、四象限,则二次函数y=ax2+bx的图象可能是( )A、 B、
B、 C、
C、 D、
D、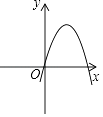 9. 如图,四边形 内接于圆 ,过 点作 于点 ,若 , ,则 的长度为( )
9. 如图,四边形 内接于圆 ,过 点作 于点 ,若 , ,则 的长度为( )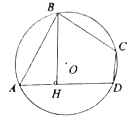 A、 B、6 C、 D、不能确定10. 如图所示, 中, , ,点 为 中点,将 绕点 旋转, 为 中点,则线段 的最小值为( )
A、 B、6 C、 D、不能确定10. 如图所示, 中, , ,点 为 中点,将 绕点 旋转, 为 中点,则线段 的最小值为( )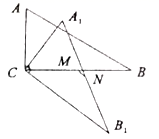 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知关于 的一元二次方程 有两个相等的实数根,则 的值是 .12. 某学生想把放置在水平桌面上的一块三角板 ( , ),绕点 按顺时针方向旋转 角,转到 的位置,其中 、 分别是 、 的对应点, 在 上(如图所示),则 角的度数为 .
 13. 已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是 .14. 如图, 是⊙ 的直径, ,点 、 在⊙ 上, 、 的延长线交于点 ,且 , ,有以下结论:① ;②劣弧 的长为 ;③点 为 的中点;④ 平分 ,以上结论一定正确的是 .
13. 已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是 .14. 如图, 是⊙ 的直径, ,点 、 在⊙ 上, 、 的延长线交于点 ,且 , ,有以下结论:① ;②劣弧 的长为 ;③点 为 的中点;④ 平分 ,以上结论一定正确的是 .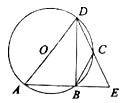
三、解答题
-
15. 解下列方程:16. 已知抛物线 经过点(1,0),(0,3).(1)、求该抛物线的函数表达式;(2)、将抛物线 平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.17. 如图, 的三个顶点坐标分别是 , , .
 (1)、将 先向左平移4个单位长度,再向上平移2个单位长度,得到 ,画出 ;(2)、 与 关于原点 成中心对称,画出 .18. 已知关于 的一元二次方程 ,(1)、求证:无论m为何值,方程总有两个不相等的实数根;(2)、当m为何值时,该方程两个根的倒数之和等于1.19. 如图所示,已知 为⊙ 的直径, 是弦,且 于点 ,连接AC、OC、BC .
(1)、将 先向左平移4个单位长度,再向上平移2个单位长度,得到 ,画出 ;(2)、 与 关于原点 成中心对称,画出 .18. 已知关于 的一元二次方程 ,(1)、求证:无论m为何值,方程总有两个不相等的实数根;(2)、当m为何值时,该方程两个根的倒数之和等于1.19. 如图所示,已知 为⊙ 的直径, 是弦,且 于点 ,连接AC、OC、BC . (1)、求证: ;(2)、若 , ,求⊙ 的直径.20. 二次函数 的图象如图所示,根据图象解答下列问题:
(1)、求证: ;(2)、若 , ,求⊙ 的直径.20. 二次函数 的图象如图所示,根据图象解答下列问题: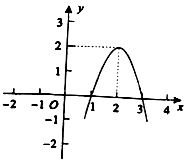 (1)、写出方程 的两个根;(2)、若方程 有两个不相等的实数根,求 的取值范围;(3)、若抛物线与直线 相交于 , 两点,写出抛物线在直线下方时 的取值范围.21. 课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.(1)、如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;(2)、如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.22. 某企业生产并销售某种产品,整理出该商品在第 ( )天的售价 与 函数关系如图所示,已知该商品的进价为每件30元,第 天的销售量为 件.
(1)、写出方程 的两个根;(2)、若方程 有两个不相等的实数根,求 的取值范围;(3)、若抛物线与直线 相交于 , 两点,写出抛物线在直线下方时 的取值范围.21. 课外活动时间,甲、乙、丙、丁4名同学相约进行羽毛球比赛.(1)、如果将4名同学随机分成两组进行对打,求恰好选中甲乙两人对打的概率;(2)、如果确定由丁担任裁判,用“手心、手背”的方法在另三人中竞选两人进行比赛.竞选规则是:三人同时伸出“手心”或“手背”中的一种手势,如果恰好只有两人伸出的手势相同,那么这两人上场,否则重新竞选.这三人伸出“手心”或“手背”都是随机的,求一次竞选就能确定甲、乙进行比赛的概率.22. 某企业生产并销售某种产品,整理出该商品在第 ( )天的售价 与 函数关系如图所示,已知该商品的进价为每件30元,第 天的销售量为 件.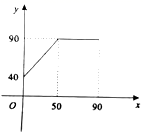 (1)、试求出售价 与 之间的函数关系是;(2)、请求出该商品在销售过程中的最大利润;(3)、在该商品销售过程中,试求出利润不低于3600元的 的取值范围.23. 在平面直角坐标系 中的两个图形 与 ,给出如下定义: 为图形 上任意一点, 为图形 上任意一点,如果 两点间的距离有最小值,那么称这个最小值为图形 间的“和睦距离”,记作 ,若图形 有公共点,则 .
(1)、试求出售价 与 之间的函数关系是;(2)、请求出该商品在销售过程中的最大利润;(3)、在该商品销售过程中,试求出利润不低于3600元的 的取值范围.23. 在平面直角坐标系 中的两个图形 与 ,给出如下定义: 为图形 上任意一点, 为图形 上任意一点,如果 两点间的距离有最小值,那么称这个最小值为图形 间的“和睦距离”,记作 ,若图形 有公共点,则 .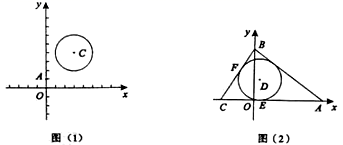 (1)、如图(1), , ,⊙ 的半径为2,则 , ;(2)、如图(2),已知 的一边 在 轴上, 在 上,且 , , .
(1)、如图(1), , ,⊙ 的半径为2,则 , ;(2)、如图(2),已知 的一边 在 轴上, 在 上,且 , , .是 内一点,若 、 分别且⊙ 于E、F,且 ,判断 与⊙ 的位置关系,并求出 点的坐标;
(3)、若以 为半径,①中的 为圆心的⊙ ,有 , ,直接写出 的取值范围 .