浙江省宁波市鄞州区七校联考2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2020-11-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列关于二次函数 $y = 2 x^{2} + 3$ ，下列说法正确的是（）.

A、它的开口方向向下 B、它的顶点坐标是 $(2, 3)$ C、当 $x < - 1$ 时， $y$ 随 $x$ 的增大而增大 D、当 $x = 0$ 时， $y$ 有最小值是3

查看试题解析
2. 一个不透明的袋中有4个白球，3个黄球和2个红球，这些球除颜色外其余都相同，则从袋中随机摸出一个球是黄球的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
3. 函数y＝x²+2x﹣4的顶点所在象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 在某校艺体节的乒乓球比赛中，李东同学顺利进入总决赛，且个人技艺高超，有同学预测“李东夺冠的可能性是80%”，对该同学的说法理解正确的是（）

A、李东夺冠的可能性较小 B、李东和他的对手比赛10局时，他一定会赢8局 C、李东夺冠的可能性较大 D、李东肯定会赢

查看试题解析
5. 下列抛物线中，与抛物线 $y = - \frac{1}{2} x^{2} - 3 x - 5$ 的形状、大小、开口方向都相等的是（）

A、 $y = \frac{1}{4} x^{2} - 7 x + 8$ B、 $y = - \frac{1}{2} x^{2} + \frac{3}{2} x - \frac{5}{2}$ C、 $y = \frac{1}{2} x^{2} + 6 x + 10$ D、 $y = - x^{2} + 3 x - 5$

查看试题解析
6. 下列关于事件发生可能性的表述，正确的是（）

A、事件：“在地面，向上抛石子后落在地上”，该事件是随机事件 B、体育彩票的中奖率为10%，则买100张彩票必有10张中奖 C、在同批次10000件产品中抽取100件发现有5件次品，则这批产品中大约有500件左右的次品 D、掷两枚硬币，朝上的一面是一正面一反面的概率为 $\frac{1}{3}$

查看试题解析
7. 如图是二次函数y＝ax²＋bx＋c的部分图象，由图象可知不等式ax²＋bx＋c<0的解集是（）

A、 $x < 5$ B、 $- 1 < x < 5$ C、 $x < - 1$ 或 $x > 5$ D、 $x < - 1$ 且 $x > 5$

查看试题解析
8. 在一个不透明的口袋中，装有3个相同的球，它们分别写有数字1，2，3，从中随机摸出一个球，若摸出的球上的数字为2的概率记 $P_{1}$ ，摸出的球上的数字小于4的记为 $P_{2}$ ，摸出的球上的数字为5的概率记为 $P_{3}$ ，则 $P_{1}$ ， $P_{2}$ ， $P_{3}$ 的大小关系是（）

A、 $P {}_{1}< P_{2} < P_{3}$ B、 $P_{3} < P_{2} < P_{1}$ C、 $P_{2} < P_{1} < P_{3}$ D、 $P_{3} < P_{1} < P_{2}$

查看试题解析
9. 某旅游景点的收入受季节的影响较大，有时候出现赔本的经营状况.因此，公司规定：若无利润时，该景点关闭.经跟踪测算，该景点一年中的利润W（万元）与月份x之间满足二次函数W=﹣x²+16x﹣48，则该景点一年中处于关闭状态有（）月.

A、5 B、6 C、7 D、8

查看试题解析
10. 已知关于 $x$ 的二次函数 $y = 3 x^{2} - 6 a x + 4 a^{2} + 2 a + 2$ ，其中 $a$ 为实数.当 $- 2 \leq x \leq 1$ 时， $y$ 的最小值为4，满足条件的 $a$ 的值为（）

A、 $- \sqrt{3} - 1$ 或 $\sqrt{3} - 1$ B、 $- \frac{5}{2}$ 或 $\sqrt{3} - 1$ C、 $- 1$ 或 $- \frac{5}{2}$ D、 $\frac{1}{2}$ 或 $\sqrt{3} - 1$

查看试题解析

二、填空题

11. 抛物线 $y = x^{2} - 4 x + 4$ 与坐标轴有个交点.

查看试题解析
12. 若将抛物线y＝3x²＋1向下平移1个单位后，则所得新抛物线的解析式是.

查看试题解析
13. 书架上有3本小说、2本散文，从中随机抽取2本都是小说的概率是.

查看试题解析
14. 如图，在平面直角坐标系中，正方形ABCD的三个顶点A、B、D均在抛物线y=ax²﹣4ax+3（a＜0）上．若点A是抛物线的顶点，点B是抛物线与y轴的交点，则AC长为．

查看试题解析
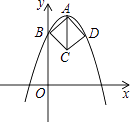15. 如图，直线AB交坐标轴于A(-2，0)，B(0，-4)，点P在抛物线 $y = \frac{1}{2} (x - 2) (x - 4)$ 上，则△ABP面积的最小值为.

查看试题解析
16. 如图，已知点 $A (3 ， 3)$ ，点 $B (0 ， 2)$ ，点 $A$ 在二次函数 $y = x^{2} + b x - 9$ 的图象上，作射线 $A B$ ，再将射线 $A B$ 绕点 $A$ 按逆时针方向旋转 $45 °$ ，交二次函数图象于点 $C$ ，则点 $C$ 的坐标为.

查看试题解析

三、解答题

17. 在湖州创建国家卫生文明城市的过程中，张辉和夏明积极参加志愿者活动，当时有下列四个志愿者工作岗位供他们选择：
①清理类岗位：清理花坛卫生死角；清理楼道杂物（分别用 $A_{1} ， A_{2}$ 表示）。
②宣传类岗位：垃圾分类知识宣传；交通安全知识宣传（分别用 $B_{1} ， B_{2}$ 表示）。

(1)、张辉同学从四个岗位中随机选取一个报名，恰好选择清理类岗位概率为是；

(2)、若张辉和夏明各随机从四个岗位中选一个报名，请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率．

查看试题解析
18. 已知二次函数y＝x²－2x－3.

(1)、求图象的开口方向、对称轴、顶点坐标；

(2)、求图象与x轴的交点坐标，与y轴的交点坐标；

(3)、当x为何值时，y随x的增大而增大？

查看试题解析
19. 平面上有3个点的坐标： $A (0 ， - 3)$ ， $B (3 ， 0)$ ， $C (- 1 ， - 4) .$

(1)、在A，B，C三个点中任取一个点，这个点既在直线 $y_{1} = x - 3$ 上又在抛物线上 $y_{2} = x^{2} - 2 x - 3$ 上的概率是多少？

(2)、从A，B，C三个点中任取两个点，求两点都落在抛物线 $y_{2} = x^{2} - 2 x - 3$ 上的概率.

查看试题解析
20. 新定义：如果二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象经过点（-1，0），那么称此二次函数的图象为“定点抛物线”

(1)、试判断二次函数 $y = 2 x^{2} - 5 x - 7$ 的图象是否为“定点抛物线”

(2)、若定点抛物线 $y = x^{2} - m x + 2 - k$ 与x轴只有一个公共点，求 $k$ 的值.

查看试题解析
21. 一名男生推铅球，铅球的行进高度 $y$ （单位： $m$ ）与水平距离 $x$ （单位： $m$ ）之间的关系为 $y = - \fra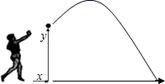c{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，铅球行进路线如图.

(1)、求出手点离地面的高度.

(2)、求铅球推出的水平距离.

(3)、通过计算说明铅球的行进高度能否达到4 $m$ .

查看试题解析
22. 某文具店销售一种进价为每本10元的笔记本，为获得高利润，以不低于进价进行销售，结果发现，每月销售量y与销售单价x之间的关系可以近似地看作一次函数：y=﹣5x+150，物价部门规定这种笔记本每本的销售单价不得高于18元.

(1)、当每月销售量为70本时，获得的利润为多少元；

(2)、该文具店这种笔记本每月获得利润为W元，求每月获得的利润W元与销售单价x之间的函数关系式，并写出自变量的取值范围；

查看试题解析
23. 定义：在平面直角坐标系xOy中，直线y＝a（x﹣m）+k称为抛物线y＝a（x﹣m）²+k的关联直线.

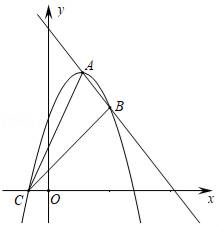(1)、求抛物线y＝x²+6x﹣1的关联直线；

(2)、已知抛物线y＝ax²+bx+c与它的关联直线y＝2x+3都经过y轴上同一点，求这条抛物线的表达式；

(3)、如图，顶点在第一象限的抛物线y＝﹣a（x﹣1）²+4a与它的关联直线交于点A，B（点A在点B的左侧），与x轴负半轴交于点C，连结AC、BC.当△ABC为直角三角形时，求a的值.

查看试题解析
24. 如图，抛物线y=ax²+bx(a＜0）过点E(10，0)，矩形ABCD的边AB在线段OE上（点A在点B的左边），点C，D在抛物线上.设A(t，0)，当t=2时，AD=4.

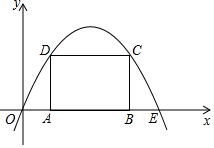(1)、求抛物线的函数表达式.

(2)、当t为何值时，矩形ABCD的周长有最大值？最大值是多少？

(3)、保持t=2时的矩形ABCD不动，向右平移抛物线.当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形的面积时，求抛物线平移的距离.

查看试题解析