安徽省铜陵市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 气象台预报“铜陵市明天降水概率是75%”.据此信息,下列说法正确的是( )A、铜陵市明天将有75%的时间降水 B、铜陵市明天将有75%的地区降水 C、铜陵市明天降水的可能性比较大 D、铜陵市明天肯定下雨3. 抛物线 的顶点坐标是( )A、(2, 1) B、(2, -1) C、(-2, 1) D、(-2, -1)4. 如图,一块含 角的直角三角板绕点 按顺时针方向,从 处旋转到 的位置,当点 、点 、点 在一条直线上时,这块三角板的旋转角度为( )
2. 气象台预报“铜陵市明天降水概率是75%”.据此信息,下列说法正确的是( )A、铜陵市明天将有75%的时间降水 B、铜陵市明天将有75%的地区降水 C、铜陵市明天降水的可能性比较大 D、铜陵市明天肯定下雨3. 抛物线 的顶点坐标是( )A、(2, 1) B、(2, -1) C、(-2, 1) D、(-2, -1)4. 如图,一块含 角的直角三角板绕点 按顺时针方向,从 处旋转到 的位置,当点 、点 、点 在一条直线上时,这块三角板的旋转角度为( ) A、60° B、120° C、150° D、180°5. 已知⊙O的直径为8cm , P为直线l上一点,OP=4cm , 那么直线l与⊙O的公共点有( )A、0个 B、1个 C、2个 D、1个或2个6. 如果 , 两点都在反比例函数 的图象上,那么 与 的大小关系是( )A、 B、 C、 D、7. 如图,正方形 中,点 是以 为直径的半圆与对角线 的交点.现随机向正方形 内投掷一枚小针,则针尖落在阴影区域的概率为( )
A、60° B、120° C、150° D、180°5. 已知⊙O的直径为8cm , P为直线l上一点,OP=4cm , 那么直线l与⊙O的公共点有( )A、0个 B、1个 C、2个 D、1个或2个6. 如果 , 两点都在反比例函数 的图象上,那么 与 的大小关系是( )A、 B、 C、 D、7. 如图,正方形 中,点 是以 为直径的半圆与对角线 的交点.现随机向正方形 内投掷一枚小针,则针尖落在阴影区域的概率为( ) A、 B、 C、 D、8. 已知关于 的方程 有一个根是 ,则 的值是( )A、-1 B、0 C、 D、19. 如图,⊙ 的半径 垂直于弦 , 是优弧 上的一点(不与点 重合),若 ,则 等于( )
A、 B、 C、 D、8. 已知关于 的方程 有一个根是 ,则 的值是( )A、-1 B、0 C、 D、19. 如图,⊙ 的半径 垂直于弦 , 是优弧 上的一点(不与点 重合),若 ,则 等于( ) A、 B、 C、 D、10. 抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示.下列叙述中:① ;②关于 的方程 的两个根是 ;③ ;④ ;⑤当 时, 随 增大而增大.正确的个数是( )
A、 B、 C、 D、10. 抛物线 的对称轴为直线 ,与 轴的一个交点坐标为 ,其部分图象如图所示.下列叙述中:① ;②关于 的方程 的两个根是 ;③ ;④ ;⑤当 时, 随 增大而增大.正确的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
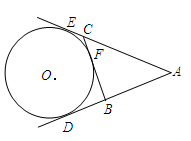
11. 如图, 、 、 均为⊙ 的切线, 分别是切点, ,则 的周长为 .
 12. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池,丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑,内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形的边长是x步,则列出的方程是.
12. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池,丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑,内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形的边长是x步,则列出的方程是.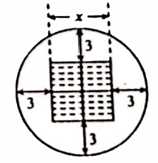 13. 已知某品牌汽车在进行刹车测试时发现,该品牌某款汽车刹车后行驶的距离 (单位:米)与行驶时间 (单位:秒)满足下面的函数关系: .那么测试实验中该汽车从开始刹车到完全停止,共行驶了米.14. 如图,半圆 的半径为4,初始状态下其直径平行于直线 .现让半圆 沿直线 进行无滑动滚动,直到半圆 的直径与直线 重合为止.在这个滚动过程中,圆心 运动路径的长度等于 .
13. 已知某品牌汽车在进行刹车测试时发现,该品牌某款汽车刹车后行驶的距离 (单位:米)与行驶时间 (单位:秒)满足下面的函数关系: .那么测试实验中该汽车从开始刹车到完全停止,共行驶了米.14. 如图,半圆 的半径为4,初始状态下其直径平行于直线 .现让半圆 沿直线 进行无滑动滚动,直到半圆 的直径与直线 重合为止.在这个滚动过程中,圆心 运动路径的长度等于 . 15. 如图,反比例函数 的图象经过点 ,过 作 轴垂线,垂足是 是 轴上任意一点,则 的面积是 .
15. 如图,反比例函数 的图象经过点 ,过 作 轴垂线,垂足是 是 轴上任意一点,则 的面积是 . 16. 如图, 中, , , , 是 上一个动点,以 为直径的⊙ 交 于 ,则线段 长的最小值是 .
16. 如图, 中, , , , 是 上一个动点,以 为直径的⊙ 交 于 ,则线段 长的最小值是 .
三、解答题
-
17. 解一元二次方程: .18. 如图,在△ABC中,∠C=60°,AB=4.以AB为直径画⊙O,交边AC于点D.AD的长为 ,求证:BC是⊙O的切线.
 19. 如图,在平面直角坐标系 中,反比例函数 的图象与一次函数 的图象的一个交点为 .
19. 如图,在平面直角坐标系 中,反比例函数 的图象与一次函数 的图象的一个交点为 . (1)、求这个反比例函数的解析式;(2)、求两个函数图象的另一个交点 的坐标;并根据图象,直接写出关于 的不等式 的解集.20. 如图,有三张不透明的卡片,除正面标记有不同数字外,其它均相同.将这三张卡片反面朝上洗匀后,从中随机抽取一张;放回洗匀后,再随机抽取一张.我们把第一次抽取的卡片上标记的数字记作 ,第二次抽取的卡片上标记的数字记作 .
(1)、求这个反比例函数的解析式;(2)、求两个函数图象的另一个交点 的坐标;并根据图象,直接写出关于 的不等式 的解集.20. 如图,有三张不透明的卡片,除正面标记有不同数字外,其它均相同.将这三张卡片反面朝上洗匀后,从中随机抽取一张;放回洗匀后,再随机抽取一张.我们把第一次抽取的卡片上标记的数字记作 ,第二次抽取的卡片上标记的数字记作 . (1)、写出k为负数的概率;(2)、求使得一次函数y=kx+b的图象经过第二、三、四象限的概率.(用树状图或列表法求解)21. 在“美丽乡村”建设中,某村施工人员想利用如图所示的直角墙角,计划再用30米长的篱笆围成一个矩形花园 ,要求把位于图中点 处的一颗景观树圈在花园内,且景观树 与篱笆的距离不小2米.已知点 到墙体 、 的距离分别是8米、16米,如果 、 所在两面墙体均足够长,求符合要求的矩形花园面积 的最大值.
(1)、写出k为负数的概率;(2)、求使得一次函数y=kx+b的图象经过第二、三、四象限的概率.(用树状图或列表法求解)21. 在“美丽乡村”建设中,某村施工人员想利用如图所示的直角墙角,计划再用30米长的篱笆围成一个矩形花园 ,要求把位于图中点 处的一颗景观树圈在花园内,且景观树 与篱笆的距离不小2米.已知点 到墙体 、 的距离分别是8米、16米,如果 、 所在两面墙体均足够长,求符合要求的矩形花园面积 的最大值. 22.(1)、(特例感知)如图①,∠ABC 是⊙O 的圆周角,BC 为直径,BD 平分∠ABC 交⊙O 于点 D,CD=3, BD=4,则点D到直线 AB 的距离为 .
22.(1)、(特例感知)如图①,∠ABC 是⊙O 的圆周角,BC 为直径,BD 平分∠ABC 交⊙O 于点 D,CD=3, BD=4,则点D到直线 AB 的距离为 . (2)、(类比迁移)
(2)、(类比迁移)如图②,∠ABC 是⊙O 的圆周角,BC 为⊙O 的弦,BD 平分∠ABC 交⊙O 于点 D,过点D作 DE⊥BC,垂足为E,探索线段 AB、BE、BC 之间的数量关系,并说明理由.
 (3)、(问题解决)
(3)、(问题解决)如图③,四边形 ABCD 为⊙O 的内接四边形,∠ABC=90°,BD 平分∠ABC,BD= 7 , AB=6,则△ABC 的内心与外心之间的距离为 .
