安徽省潜山市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 抛物线 的对称轴是( )A、 B、 C、 D、2. 若函数 其几对对应值如下表,则方程 ( , , 为常数)根的个数为( )
-2
-1
1
1
-1
1
A、0 B、1 C、2 D、1或23. 若点 、 、 都在反比例函数 的图象上,并且 ,则下列各式中正确的是( )A、 B、 C、 D、4. 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A、4cm B、6cm C、8cm D、10cm5. 如图,在 中,D、E分别在AB边和AC边上, ,M为BC边上一点(不与B,C重合),连结AM交DE于点N,则( )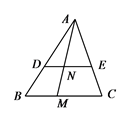 A、 B、 C、 D、6. 如图,⊙ 是 的外接圆,已知 平分 交⊙ 于点 ,交 于点 ,若 , ,则 的长为( )
A、 B、 C、 D、6. 如图,⊙ 是 的外接圆,已知 平分 交⊙ 于点 ,交 于点 ,若 , ,则 的长为( ) A、 B、 C、 D、7. 如图,在 中, , ,折叠 使得点 落在 边上的点 处,折痕为 . 连接 、 ,下列结论:①△ 是等腰直角三角形;② ;③ ;④ .其中正确的个数是( )
A、 B、 C、 D、7. 如图,在 中, , ,折叠 使得点 落在 边上的点 处,折痕为 . 连接 、 ,下列结论:①△ 是等腰直角三角形;② ;③ ;④ .其中正确的个数是( ) A、1 B、2 C、3 D、48. 如图,已知正方形ABCD , 将对角线BD绕着点B逆时针旋转,使点D落在CB的延长线上的D′点处,那么sin∠AD′B的值是( )
A、1 B、2 C、3 D、48. 如图,已知正方形ABCD , 将对角线BD绕着点B逆时针旋转,使点D落在CB的延长线上的D′点处,那么sin∠AD′B的值是( )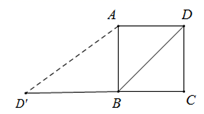 A、 B、 C、 D、9. 如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m 远,该同学的身高为1.7m ,则树高为( ).
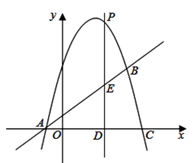
A、 B、 C、 D、9. 如图,一同学在湖边看到一棵树,他目测出自己与树的距离为20m,树的顶端在水中的倒影距自己5m 远,该同学的身高为1.7m ,则树高为( ).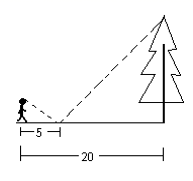 A、3.4m B、4.7 m C、5.1m D、6.8m10. 二次函数 的图象如图所示,其对称轴为 ,有下列结论:① ;② ;③ ;④对任意的实数 ,都有 ,其中正确的是( )
A、3.4m B、4.7 m C、5.1m D、6.8m10. 二次函数 的图象如图所示,其对称轴为 ,有下列结论:① ;② ;③ ;④对任意的实数 ,都有 ,其中正确的是( ) A、①② B、①④ C、②③ D、②④
A、①② B、①④ C、②③ D、②④二、填空题
-
11. 直线y=2被抛物线y=x2﹣3x+2截得的线段长为.12. 我军侦察员在距敌方120m的地方发现敌方的一座建筑物,但不知其高度又不能靠近建筑物物测量,机灵的侦察员将自己的食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住,如图所示.若此时眼睛到食指的距离约为40cm,食指的长约为8cm,则敌方建筑物的高度约是m.
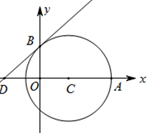
 13. 如图,AB是圆O的弦,AB=20 ,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN的最大值是 .
13. 如图,AB是圆O的弦,AB=20 ,点C是圆O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN的最大值是 .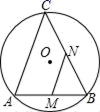 14. 如图,已知点A,C在反比例函数 的图象上,点B,D在反比例函 的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=5,CD=4,AB与CD的距离为6,则a−b的值是.
14. 如图,已知点A,C在反比例函数 的图象上,点B,D在反比例函 的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=5,CD=4,AB与CD的距离为6,则a−b的值是.
三、解答题
-
15. 计算:﹣12019+| ﹣2|+2cos30°+(2﹣tan60°)0 .16. 如图,已知 是原点, 两点的坐标分别为 , .
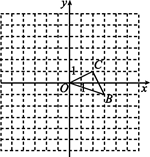 (1)、以点 为位似中心,在 轴的左侧将 扩大为原来的两倍(即新图与原图的相似比为 ),画出图形,并写出点 的对应点的坐标;(2)、如果 内部一点 的坐标为 ,写出点 的对应点 的坐标.17. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(-3,m+8),B(n,-6)两点.
(1)、以点 为位似中心,在 轴的左侧将 扩大为原来的两倍(即新图与原图的相似比为 ),画出图形,并写出点 的对应点的坐标;(2)、如果 内部一点 的坐标为 ,写出点 的对应点 的坐标.17. 如图,一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(-3,m+8),B(n,-6)两点.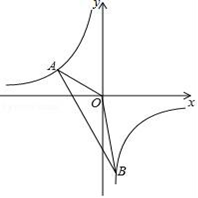 (1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积.18. 如图,在某建筑物 上,挂着“缘分天注定,悠然在潜山”的宣传条幅 ,小明站在点 处,看条幅顶端 ,测得仰角为 ,再往条幅方向前行30米到达点 处,看到条幅顶端 ,测得仰角为 ,求宣传条幅 的长.(注:不计小明的身高,结果精确到1米,参考数据 , )
(1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积.18. 如图,在某建筑物 上,挂着“缘分天注定,悠然在潜山”的宣传条幅 ,小明站在点 处,看条幅顶端 ,测得仰角为 ,再往条幅方向前行30米到达点 处,看到条幅顶端 ,测得仰角为 ,求宣传条幅 的长.(注:不计小明的身高,结果精确到1米,参考数据 , )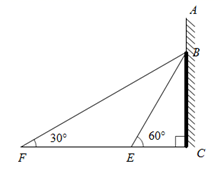 19. 如图, , 分别是 , 上的点, , 于 , 于 .若 , ,求:
19. 如图, , 分别是 , 上的点, , 于 , 于 .若 , ,求: (1)、 ;(2)、 与 的面积比.20. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)、 ;(2)、 与 的面积比.20. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)、求w与x之间的函数关系式.(2)、该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?21. 如图,在正方形 中, 为边 的中点,点 在边 上,且 ,延长 交 的延长线于点 .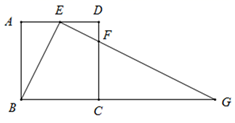 (1)、求证:△ ∽△ .(2)、若 ,求 的长.
(1)、求证:△ ∽△ .(2)、若 ,求 的长.