安徽省淮北市濉溪县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 已知 ,则下列比例式成立的是( )A、 B、 C、 D、2. 在 中, , ,则 的值是( )A、 B、 C、 D、3. 给出下列四个函数:①y=﹣x;②y=x;③y= ;④y=x2 . x<0时,y随x的增大而减小的函数有( )A、1个 B、2个 C、3个 D、4个4. 如图,△ABC∽△ADE , 则下列比例式正确的是( )
 A、 B、 C、 D、5. 如图,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A、 B、 C、 D、5. 如图,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( ) A、30° B、40° C、50° D、60°6. 二次函数 化为 的形式,结果正确的是( )A、 B、 C、 D、7. 已知 ,则锐角 的取值范围是( )A、 B、 C、 D、8. 反比例函数 图象上的两点为 , 且 ,则下列表达式成立的是( )A、 B、 C、 D、不能确定9. 如图,在四边形 中, ,对角线 、 交于点 有以下四个结论其中始终正确的有( )
A、30° B、40° C、50° D、60°6. 二次函数 化为 的形式,结果正确的是( )A、 B、 C、 D、7. 已知 ,则锐角 的取值范围是( )A、 B、 C、 D、8. 反比例函数 图象上的两点为 , 且 ,则下列表达式成立的是( )A、 B、 C、 D、不能确定9. 如图,在四边形 中, ,对角线 、 交于点 有以下四个结论其中始终正确的有( )
① ; ② ;③ ; ④
A、1个 B、2个 C、3个 D、4个10. 如图,点 是以 为直径的半圆上的动点, 于点 ,连接 ,设 ,则下列函数图象能反映 与 之间关系的是( )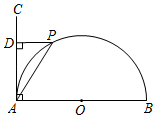 A、
A、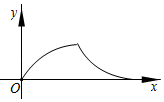 B、
B、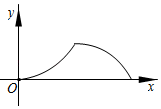 C、
C、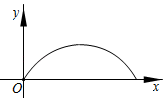 D、
D、
二、填空题
-
11. 已知二次函数 的图象与x轴有交点,则k的取值范围是12. 如图,电灯 在横杆 的正上方, 在灯光下的影子为 , , 米, 米,点 到 的距离是3米,则 到 的距离是米.
 13. 如图,在 中,弦 ,点 在 上移动,连结 ,过点 作 交 于点 ,则 的最大值为 .
13. 如图,在 中,弦 ,点 在 上移动,连结 ,过点 作 交 于点 ,则 的最大值为 . 14. 一张直角三角形纸片 , , , ,点 为 边上的任一点,沿过点 的直线折叠,使直角顶点 落在斜边 上的点 处,当 是直角三角形时,则 的长为 .
14. 一张直角三角形纸片 , , , ,点 为 边上的任一点,沿过点 的直线折叠,使直角顶点 落在斜边 上的点 处,当 是直角三角形时,则 的长为 .三、解答题
-
15. 计算 的值.16. 已知抛物线 的对称轴为直线 ,且经过点(1)、求抛物线的表达式;(2)、请直接写出 时 的取值范围.17. 如图,在平面直角坐标系中, 的三个顶点坐标分别为 , ,
 (1)、画出 关于 轴对称的 ,并写出点 的坐标;(2)、画出 绕原点 顺时针方向旋转 后得到的 ,并写出点 的坐标;(3)、将 平移得到 ,使点 的对应点是 ,点 的对应点时 ,点 的对应点是 ,在坐标系中画出 ,并写出点 , 的坐标.18. 如图,在平面直角坐标系 中,一次函数 的图像与反比例函数 的图像在第二象限交于点 ,与 轴交于点 ,点 在 轴上,满足条件: ,且 ,点 的坐标为 , 。
(1)、画出 关于 轴对称的 ,并写出点 的坐标;(2)、画出 绕原点 顺时针方向旋转 后得到的 ,并写出点 的坐标;(3)、将 平移得到 ,使点 的对应点是 ,点 的对应点时 ,点 的对应点是 ,在坐标系中画出 ,并写出点 , 的坐标.18. 如图,在平面直角坐标系 中,一次函数 的图像与反比例函数 的图像在第二象限交于点 ,与 轴交于点 ,点 在 轴上,满足条件: ,且 ,点 的坐标为 , 。 (1)、求反比例函数的表达式;(2)、直接写出当 时, 的解集。19. 小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).
(1)、求反比例函数的表达式;(2)、直接写出当 时, 的解集。19. 小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示). 20. 如图, 内接于 , , 是 的弦,与 相交于点 , 平分 ,过点 作 ,分别交 , 的延长线于点 、 ,连接 .
20. 如图, 内接于 , , 是 的弦,与 相交于点 , 平分 ,过点 作 ,分别交 , 的延长线于点 、 ,连接 . (1)、求证: 是 的切线;(2)、求证: .
(1)、求证: 是 的切线;(2)、求证: .

