浙江省温州市瑞安市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 下列各组数可能是一个三角形的边长的是( )A、5,7,12 B、5,6,7 C、5,5,12 D、1,2,62. 在平面直角坐标系中,点(3,-4)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列图案中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 一次函数 的图象与 轴的交点坐标是( )A、 B、 C、 D、5. 下列选项中,可以用来说明命题“若 ,则 ”属于假命题的反例是( )A、 , B、 , C、 , D、 ,6. 直线 上有三个点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、7. 如图, ,要说明 ,需添加的条件不能是( )
4. 一次函数 的图象与 轴的交点坐标是( )A、 B、 C、 D、5. 下列选项中,可以用来说明命题“若 ,则 ”属于假命题的反例是( )A、 , B、 , C、 , D、 ,6. 直线 上有三个点 , , ,则 , , 的大小关系是( )A、 B、 C、 D、7. 如图, ,要说明 ,需添加的条件不能是( )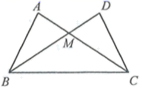 A、 B、 C、 D、8. 如图,在 中, , 是 的平分线,若 , ,则 为( )
A、 B、 C、 D、8. 如图,在 中, , 是 的平分线,若 , ,则 为( )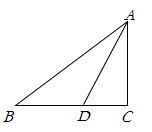 A、5:3 B、5:4 C、4:3 D、3:59. 若不等式组 的解为 ,则下列各式中正确的是( )A、 B、 C、 D、10. 意大利文艺复兴时期的著名画家达•芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形 由两个正方形和两个全等的直角三角形组成.已知六边形 的面积为28, .小明将纸片②翻转后拼成如图2所示的图形,其中 ,则四边形 的面积为( )
A、5:3 B、5:4 C、4:3 D、3:59. 若不等式组 的解为 ,则下列各式中正确的是( )A、 B、 C、 D、10. 意大利文艺复兴时期的著名画家达•芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形 由两个正方形和两个全等的直角三角形组成.已知六边形 的面积为28, .小明将纸片②翻转后拼成如图2所示的图形,其中 ,则四边形 的面积为( )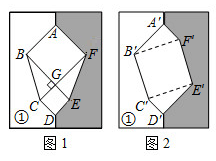 A、16 B、20 C、22 D、24
A、16 B、20 C、22 D、24二、填空题
-
11. 若 的3倍与2的差是负数,则可列出不等式.12. 把点 先向右平移2个单位,再向上平移3个单位,所得点的坐标为.13. 在 中, , 为斜边 的中点, ,则 .14. 点 关于 轴的对称点恰好落在一次函数 的图象上,则 .15. 如图,在 中, , , 分别为边 , 上一点, .将 沿 折叠,使点 与 重合,折痕交边 于点 .若 为等腰三角形,则 的度数为度.
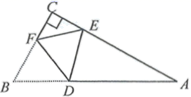 16. 图1是小慧在“天猫•双11”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚 分米, 分米, 为 上固定连接点,靠背 分米.档位为Ⅰ档时, ,档位为Ⅱ档时, .当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端 向后靠的水平距离(即 )为分米.
16. 图1是小慧在“天猫•双11”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚 分米, 分米, 为 上固定连接点,靠背 分米.档位为Ⅰ档时, ,档位为Ⅱ档时, .当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端 向后靠的水平距离(即 )为分米.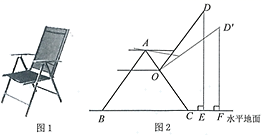
三、解答题
-
17.(1)、解不等式 ,并把解表示在数轴上.
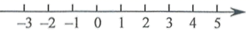 (2)、解不等式组 .18. 如图,已知 , , .
(2)、解不等式组 .18. 如图,已知 , , .求证: .
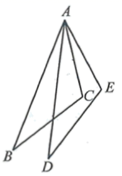 19. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形) 的顶点 , 的坐标分别为 , .
19. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形) 的顶点 , 的坐标分别为 , .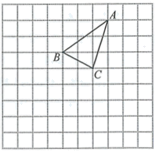 (1)、请在图中画出平面直角坐标系;(2)、请画出 关于 轴对称的 ;(3)、线段 的长为.20. 如图,直线 : 交 轴于点 ,直线 交 轴于点 , 与 的交点 的横坐标为1,连结 .
(1)、请在图中画出平面直角坐标系;(2)、请画出 关于 轴对称的 ;(3)、线段 的长为.20. 如图,直线 : 交 轴于点 ,直线 交 轴于点 , 与 的交点 的横坐标为1,连结 .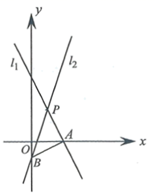 (1)、求直线 的函数表达式;(2)、求 的面积.21. 如图,在等腰 中, ,延长 至点 ,连结 ,过点 作 于点 , 为 上一点, ,连结 , .
(1)、求直线 的函数表达式;(2)、求 的面积.21. 如图,在等腰 中, ,延长 至点 ,连结 ,过点 作 于点 , 为 上一点, ,连结 , . (1)、求证: .(2)、若 , ,求 的周长.22. 某甜品店用 , 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品 份,乙款甜品 份,共用去 原料2000克.
(1)、求证: .(2)、若 , ,求 的周长.22. 某甜品店用 , 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品 份,乙款甜品 份,共用去 原料2000克.原料
款式
原料
(克)
原料
(克)
甲款甜品
30
15
乙款甜品
10
20
(1)、求 关于 的函数表达式;(2)、已知每份甲甜品的利润为5元,每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元,则至少要用去 原料多少克?23. 如图,直线 分别与 轴, 轴交于点 , ,过点 的直线 交 轴于点 . 为 的中点, 为射线 上一动点,连结 , ,过 作 于点 .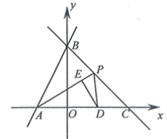 (1)、直接写出点 , 的坐标: ( , ), ( , );(2)、当 为 中点时,求 的长;(3)、当 是以 为腰的等腰三角形时,求点 坐标;(4)、当点 在线段 (不与 , 重合)上运动时,作 关于 的对称点 ,若 落在 轴上,则 的长为.
(1)、直接写出点 , 的坐标: ( , ), ( , );(2)、当 为 中点时,求 的长;(3)、当 是以 为腰的等腰三角形时,求点 坐标;(4)、当点 在线段 (不与 , 重合)上运动时,作 关于 的对称点 ,若 落在 轴上,则 的长为.