安徽省阜阳市颍州区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 与y=2(x﹣1)2+3形状相同的抛物线解析式为( )A、y=1+x2 B、y=(2x+1)2 C、y=(x﹣1)2 D、y=2x22. 如图,点 是反比例函数 的图象上任意一点,过点 作 轴,垂足为 . 连接 . 若 的面积等于2. 5,则 的值等于 ( )
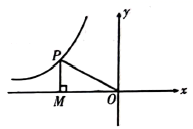 A、-5 B、5 C、-2.5 D、2.53. 下列事件是必然事件的是( )A、如果 ,那么 B、平分弦的直径垂直于弦,并且平分弦所对的两条弧 C、抛出的篮球会下落 D、三角形的内角和是4. 如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A、-5 B、5 C、-2.5 D、2.53. 下列事件是必然事件的是( )A、如果 ,那么 B、平分弦的直径垂直于弦,并且平分弦所对的两条弧 C、抛出的篮球会下落 D、三角形的内角和是4. 如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )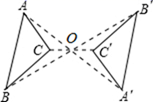 A、点A与点 是对称点 B、 C、 D、5. 一元二次方程(x-1)2=2的解是( )A、x 1 =-1- ,x 2 =-1+ B、x 1 =1- ,x 2 =1+ C、x 1 =3,x 2 =-1 D、x 1 =1,x 2 =-36. 若一元二次方程x2﹣2x﹣m=0无实数根,则反比例函数y= 的图象所在的象限是( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限7. 已知二次函数 的 与 的部分对应值如表:
A、点A与点 是对称点 B、 C、 D、5. 一元二次方程(x-1)2=2的解是( )A、x 1 =-1- ,x 2 =-1+ B、x 1 =1- ,x 2 =1+ C、x 1 =3,x 2 =-1 D、x 1 =1,x 2 =-36. 若一元二次方程x2﹣2x﹣m=0无实数根,则反比例函数y= 的图象所在的象限是( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限7. 已知二次函数 的 与 的部分对应值如表:-1
0
2
3
4
5
0
-4
-3
0
下列结论: 抛物线的开口向上;②抛物线的对称轴为直线 ;③当 时, ;④抛物线与 轴的两个交点间的距离是 ;⑤若 是抛物线上两点,则 ,其中正确的个数是( )
A、2 B、3 C、4 D、58. 如图, 是 的内接三角形, ,过点 的圆的切线交 于点 ,则 的度数为( )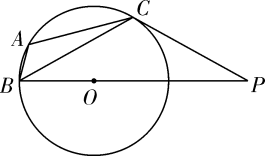 A、32° B、31° C、29° D、61°9. 某商场销售额3月份为16万元,5月份为25万元,该商场这两个月销售额的平均增长率是( )A、 B、 C、 D、10. 学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )A、 B、 C、 D、
A、32° B、31° C、29° D、61°9. 某商场销售额3月份为16万元,5月份为25万元,该商场这两个月销售额的平均增长率是( )A、 B、 C、 D、10. 学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是( )A、 B、 C、 D、二、填空题
-
11. “任意打开我们的九上数学书,正好是第60页”,这是(选填“随机”或“必然”)事件.12. 一副三角板如图放置,将三角板ADE绕点A逆时针旋转 ,使得三角板ADE的一边所在的直线与BC垂直,则 的度数为.
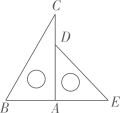 13. 如图, 为 的直径, 为 外一点,过点 作 的切线,切点为 ,连接 交 于点 , . 点 在 右侧的半圆周上运动(不与 重合),则 的度数是.
13. 如图, 为 的直径, 为 外一点,过点 作 的切线,切点为 ,连接 交 于点 , . 点 在 右侧的半圆周上运动(不与 重合),则 的度数是.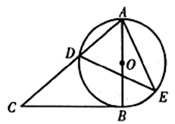
三、解答题
-
14. 抛物线 的图象如图所示,则抛物线的对称轴为直线.
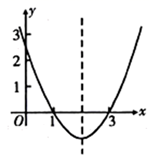 15. 解方程: .16. 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m .(1)、求动力F与动力臂l的函数解析式;(2)、当动力臂为1.5m时,撬动石头至少需要多大的力?17. 已知二次函数的解析式是 .
15. 解方程: .16. 小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m .(1)、求动力F与动力臂l的函数解析式;(2)、当动力臂为1.5m时,撬动石头至少需要多大的力?17. 已知二次函数的解析式是 .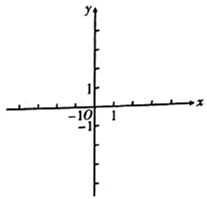 (1)、在直角坐标系中,画出它的图象,求 为何值时,函数值 ;(2)、当 时,观察图象直接写出函数值 的取值范围.18. 如图,有一块矩形硬纸板,长 ,宽 .在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为 ?
(1)、在直角坐标系中,画出它的图象,求 为何值时,函数值 ;(2)、当 时,观察图象直接写出函数值 的取值范围.18. 如图,有一块矩形硬纸板,长 ,宽 .在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为 ?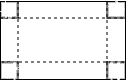 19. 如图,一次函数y=kx+b的图象与反比例函数 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
19. 如图,一次函数y=kx+b的图象与反比例函数 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.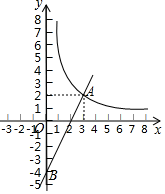 (1)、求函数 和y=kx+b的解析式;(2)、结合图象直接写出不等式组0< <kx+b的解集.20. 如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)、求函数 和y=kx+b的解析式;(2)、结合图象直接写出不等式组0< <kx+b的解集.20. 如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).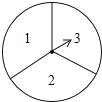
(1)、请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)、求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.
21. 如图,每个小正方形的边长均为1个单位长度, 在平面直角坐标系中,顶点的坐标分别为 .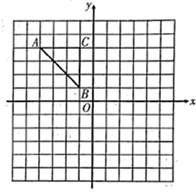 (1)、画出 关于 轴对称的 ;(2)、将 绕点 逆时针旋转 ,得到 ,画出 ;(3)、在(2)的条件下,求线段 在旋转过程中扫过的图形面积. (结果保留 )22. 某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量 与时间第 天之间的函数关系式为 ( , 为整数),销售单价 (元/ )与时间第 天之间满足一次函数关系如下表:
(1)、画出 关于 轴对称的 ;(2)、将 绕点 逆时针旋转 ,得到 ,画出 ;(3)、在(2)的条件下,求线段 在旋转过程中扫过的图形面积. (结果保留 )22. 某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量 与时间第 天之间的函数关系式为 ( , 为整数),销售单价 (元/ )与时间第 天之间满足一次函数关系如下表:时间第 天
1
2
3
…
80
销售单价 (元/ )
49. 5
49
48. 5
…
10
(1)、写出销售单价 (元/ )与时间第 天之间的函数关系式;(2)、在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?23. 如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且 = ,连接GO并延长交⊙O于点F,连接BF.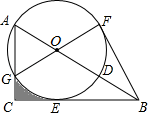 (1)、求证:①AO=AG.②BF是⊙O的切线.(2)、若BD=6,求图形中阴影部分的面积.
(1)、求证:①AO=AG.②BF是⊙O的切线.(2)、若BD=6,求图形中阴影部分的面积.