浙江省台州市玉环市2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-11-02 类型：期末考试

进入出卷网下载

一、选择题

1. 下列四个数学符号中，是轴对称图形的是（）

A、 $⊥$ B、 $≌$ C、 D、

查看试题解析
2. 估算 $\sqrt{75}$ 在（）

A、5与6之间 B、6与7之间 C、7与8之间 D、8与9之间

查看试题解析
3. 计算 $(- x + y) (x + y)$ 的结果是（）

A、 $x^{2} - y^{2}$ B、 $- x^{2} + y^{2}$ C、 $- x^{2} - y^{2}$ D、 $x^{2} + y^{2}$

查看试题解析
4. 如图，在一张长方形的纸板上找一点 $P$ ，使它到 $A B$ ， $A D$ 的距离相等，且到点 $B$ ， $C$ 的距离也相等，则下列作法正确的是（）

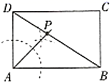A、 B、、 C、 D、

查看试题解析
5. 下列各式从左到右的变形正确的是（）

A、 $\frac{a}{b} = \frac{a + 1}{b + 1}$ B、 $\frac{- a + c}{b} = - \frac{a + c}{b}$ C、 $\frac{a - b}{c + d} = \frac{a + b}{c - d}$ D、 $\frac{2 a + 2 b}{{(a + b)}^{2}} = \frac{2}{a + b}$

查看试题解析
6. 如图是某商场一楼与二楼之间的手扶电梯示意图.其中 $A B$ 、 $C D$ 分别表示一楼、二楼地面的水平线， $∠ A B C = 150 °$ ， $B C$ 的长是 $40 m$ ，则乘电梯从点 $B$ 到点 $C$ 上升的高度 $h$ 是（）

A、 $20 m$ B、 $\frac{20}{3} \sqrt{3} m$ C、 $\frac{40}{3} \sqrt{3} m$ D、 $20 \sqrt{3} m$

查看试题解析
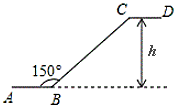7. 已知 $a$ ， $b$ ， $c$ 为 $Δ A B C$ 三边，且满足 $a b + b c = b^{2} + a c$ 则 $Δ A B C$ 是（）

A、直角三角形 B、等边三角形 C、等腰三角形 D、不能确定

查看试题解析
8. 世界文化遗产“三孔”景区已经完成5G基站布设，“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍，在峰值速率下传输500兆数据，5G 网络比4G 网络快45秒，求这两种网络的峰值速率．设4G网络的峰值速率为每秒传输 $x$ 兆数据，依题意，可列方程是（）

A、 $\frac{500}{x} - \frac{500}{10 x} = 45$ B、 $\frac{500}{10 x} - \frac{500}{x} = 45$ C、 $\frac{5000}{x} - \frac{500}{x} = 45$ D、 $\frac{500}{x} - \frac{5000}{x} = 45$

查看试题解析
9. 已知 $a$ ， $b$ ， $c$ ， $d$ 都是正数，且 $a^{2} = 2$ ， $b^{3} = 3$ ， $c^{4} = 4$ ， $d^{5} = 5$ ，则 $a$ ， $b$ ， $c$ ， $d$ 从小到大排列正确的是（）

A、 $a < b < c < d$ B、 $b < a = c < d$ C、 $d < c < b < a$ D、 $d < c = a < b$

查看试题解析
10. 四个形状大小相同的等腰三角形按如图所示方式摆放，已知 $∠ A O B = ∠ A O C = 90 °$ ， $E F = 2 cm$ ，若点 $F$ 落在 $B G$ 的延长线上，则图中阴影部分的面积为（）

A、 $(4 \sqrt{2} + 4) {cm}^{2}$ B、 $(4 \sqrt{3}) {cm}^{2}$ C、 $(2 \sqrt{2} + 8) {cm}^{2}$ D、 $(2 \sqrt{3} + 8) {cm}^{2}$

查看试题解析

二、填空题

11. 分解因式：3x²-6x=.

查看试题解析
12. 要使代数式 $\sqrt{x^{2} + 1} + \sqrt{1 - x}$ 有意义，则 $x$ 的取值范围为.

查看试题解析
13. 如图，在△ABC中，∠ACB=60°，∠BAC=75°，AD⊥BC于D，BE⊥AC于E，AD与BE交于H，则∠CHD=

查看试题解析
14. 图1是小明家围墙的一部分，上部分是由不锈钢管焊成的等腰三角形栅栏，底边上等距焊上一些立柱，请你根据图2所标注的尺寸，求焊成一个等腰三角形栅栏（图2中的实线部分）至少需要不锈钢管米（焊接部分忽略不计）.

查看试题解析
15. 设 $a \neq b$ ，我们用符号 $[a ， b]$ 表示两数中较大的一个，如 $[\frac{1}{7} ， - 2] = \frac{1}{7}$ ，按照这个规定：方程 $[\frac{1 - x}{x - 4} ， - 2] = \frac{5 - 2 x}{4 - x}$ 的解为.

查看试题解析
16. 如图，在等腰直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 4$ ， $D$ 为 $B C$ 中点， $E$ 为 $A C$ 边上一动点，连接 $D E$ ，以 $D E$ 为边并在 $D E$ 的右侧作等边 $Δ D E F$ ，连接 $B F$ ，则 $B F$ 的最小值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{12} - \sqrt{27} + \sqrt{3}$

(2)、 ${(- 2 a b^{2})}^{3} + (2 a^{2} b) (- 3 a b^{5})$

查看试题解析
18. 在正方形网格中，每个小正方形的顶点称为格点.

(1)、如图① $8 \times 8$ 的正方形网格中，线段 $O M$ 、 $O N$ 的端点均在格点上，在给定的网格中以 $O M$ 、 $O N$ 为邻边画一个四边形，使第四个顶点在格点上，所画的四边形是轴对称图形；

(2)、如图② $5 \times 5$ 的正方形网格中，画出以 $A B$ 为斜边的直角三角形 $Δ A B C$ .要求：顶点在格点上，且各边的长均为无理数.

查看试题解析
19. 先化简，再求值： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，其中x=3．

查看试题解析
20. 如图，AD⊥AB，DE⊥AE，BC⊥AE，垂足分别为A、E、C，且AD＝AB，求证：△AED≌△BCA.

查看试题解析
21. 小明家在“吾悦广场”购买了一间商铺，准备承包给甲、乙两家装修公司进行店面装修，经调查：甲公司单独完成该工程的时间是乙公司的2倍，已知甲、乙两家公司共同完成该工程建设需20天；若甲公司每天所需工作费用为650元，乙公司每天所需工作费用为1200元，若从节约资金的角度考虑，则应选择哪家公司更合算？

查看试题解析
22. 小迪同学在学勾股定理时发现一类特殊三角形：在一个三角形中，如果一个角是另一个角的2倍，那么称这个三角形为“倍角三角形”.
如图1，在倍角 $Δ A B C$ 中， $∠ A = 2 ∠ B$ ， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边分别记为 $a$ ， $b$ ， $c$ ，三角形的三边 $a$ ， $b$ ， $c$ 有什么关系呢？让我们一起来探索……

(1)、已知“倍角三角形”的一个内角为 $150 °$ ，则这个三角形的另两个角的度数分别为

(2)、小迪同学先从特殊的“倍角三角形”入手研究，请你结合图2和图3填写下表：

三角形

角的已知量

$\frac{a}{b}$

$\frac{b + c}{a}$

图2

$∠ A = 2 ∠ B = 90 °$

图3

$∠ A = 2 ∠ B = 60 °$

小迪同学根据上表，提出一般性猜想：在“倍角三角形”中， $∠ A = 2 ∠ B$ ，那么 $a$ ， $b$ ， $c$ 三边满足：；

(3)、如图1：在倍角三角形中， $∠ A = 2 ∠ B = 30 °$ ， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的对边分别记为 $a$ ， $b$ ， $c$ ，求证： $a^{2} - b^{2} = b c$ .

查看试题解析
23. 根据同底数幂的乘法法则，我们发现： $a^{m + n} = a^{m} \cdot a^{n}$ （其中 $a \neq 0$ ， $m$ ， $n$ 为正整数），类似地我们规定关于任意正整数 $m$ ， $n$ 的一种新运算： $h (m + n) = h (m) \cdot h (n)$ ，请根据这种新运算解决以下问题：

(1)、若 $h (1) = - 1$ ，则 $h (2) =$ ； $h (2019) =$ ；

(2)、若 $h (7) = 128$ ，求 $h (2)$ ， $h (8)$ 的值；

(3)、若 $\frac{h (4)}{h (2)} = 4$ ，求 $h (2)$ 的值；

(4)、若 $\frac{h (4)}{h (2)} = 4$ ，直接写出 $\frac{h (2)}{h (1)} + \frac{h (4)}{h (2)} + \frac{h (6)}{h (3)} + \dots + \frac{h (2 n)}{h (n)}$ 的值.

查看试题解析
24.

(1)、（问题背景）
如图1，等腰 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ，则 $\frac{B C}{A B} =$ ；

(2)、（知识应用）
如图2， $Δ A B C$ 和 $Δ A D E$ 都是等腰三角形， $∠ B A C = ∠ D A E = 120 °$ ， $D$ 、 $E$ 、 $C$ 三点在同一条直线上，连接 $B D$ .

①求证： $Δ A D B ≌ Δ A E C$ ；

②请写出线段 $A D$ ， $B D$ ， $C D$ 之间的等量关系式，并说明理由？

(3)、如图3， $Δ A B D$ 和 $Δ C B D$ 均为等边三角形，在 $∠ A B C$ 内作射线 $B M$ ，作点 $C$ 关于 $B M$ 的对称点 $E$ ，连接 $A E$ 并延长交 $B M$ 于点 $F$ ，连接 $C E$ ， $C F$ .若 $A E = 4$ ， $C E = 1$ ，求 $B F$ 的长.

查看试题解析

三角形	角的已知量	$\frac{a}{b}$	$\frac{b + c}{a}$
图2	$∠ A = 2 ∠ B = 90 °$
图3	$∠ A = 2 ∠ B = 60 °$