安徽省阜阳市临泉县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 抛物线y=x2﹣2x+2的顶点坐标为( )A、(1,1) B、(﹣1,1) C、(1,3) D、(﹣1,3)2. 在 中, ,则 的正切值为( )A、3 B、 C、 D、3. 已知 ,下列变形错误的是( )
A、 B、 C、 D、4. 某学校要种植一块面积为100m2的长方形草坪,要求两边长均不小于5m,则草坪的一边长为y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )A、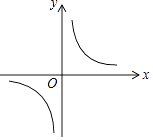 B、
B、 C、
C、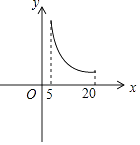 D、
D、 5. 在 中, 是 边上的点, ,则 的长为( )A、6 B、7 C、8 D、96. 已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )A、3:5 B、9:25 C、5:3 D、25:97. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )
5. 在 中, 是 边上的点, ,则 的长为( )A、6 B、7 C、8 D、96. 已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是( )A、3:5 B、9:25 C、5:3 D、25:97. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )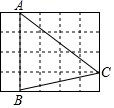 A、 B、 C、 D、8. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( )
A、 B、 C、 D、8. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( ) A、①④ B、①② C、②③④ D、②③9. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )
A、①④ B、①② C、②③④ D、②③9. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )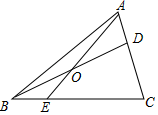 A、1:2 B、1:3 C、1:4 D、2:310. 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象大致形状是( )
A、1:2 B、1:3 C、1:4 D、2:310. 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象大致形状是( ) A、
A、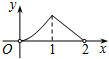 B、
B、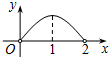 C、
C、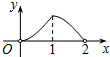 D、
D、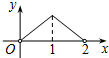
二、填空题
-
11. 若 ,且 ,则a-b的值是 .12. 如图,在 中,点 在 上,请再添加一个适当的条件,使 与 相似,那么要添加的条件是 . (只填一个即可)
 13. 如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B=度.
13. 如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B=度. 14. 在△ABC中,∠ABC=90°,已知AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交直线AB于点P,当△PQB为等腰三角形时,线段AP的长为 .15. 如图,矩形 的顶点 , 在反比例函数 的图象上,若点 的坐标为 , , 轴,则点 的坐标为.
14. 在△ABC中,∠ABC=90°,已知AB=3,BC=4,点Q是线段AC上的一个动点,过点Q作AC的垂线交直线AB于点P,当△PQB为等腰三角形时,线段AP的长为 .15. 如图,矩形 的顶点 , 在反比例函数 的图象上,若点 的坐标为 , , 轴,则点 的坐标为.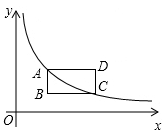 16. 如图,在△ABC中,点DE分别在ABAC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6.则线段CD的长为
16. 如图,在△ABC中,点DE分别在ABAC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6.则线段CD的长为
三、解答题
-
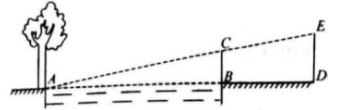
17. 计算: .18. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A , 在他们所在的岸边选择了点B , 使得AB与河岸垂直,并在B点竖起标杆BC , 再在AB的延长线上选择点D竖起标杆DE , 使得点E与点C、A共线.
已知:CB⊥AD , ED⊥AD , 测得BC=1m , DE=1.5m , BD=8.5m . 测量示意图如图所示.请根据相关测量信息,求河宽AB .
 19. 如图,在平面直角坐标系中, 的顶点坐标分别为 (每个方格的边长均为1个单位长度).
19. 如图,在平面直角坐标系中, 的顶点坐标分别为 (每个方格的边长均为1个单位长度).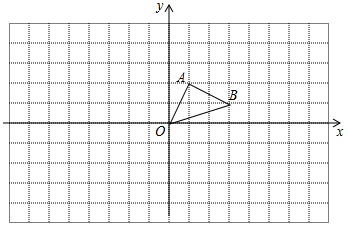 (1)、将 以点 为旋转中心,逆时针旋转 度得到 ,请画出 ;(2)、请以点 为位似中心,画出 的位似三角形 ,使相似比为 .20. 如图,在淮河的右岸边有一高楼,左岸边有一坡度 的山坡 ,点 与点 在同一水平面上, 与 在同一平面内.某数学兴趣小组为了测量楼 的高度,在坡底 处测得楼顶 的仰角为 ,然后沿坡面 上行了 米到达点 处,此时在 处测得楼顶 的仰角为 ,求楼 的高度.(结果保留整数)(参考数 )
(1)、将 以点 为旋转中心,逆时针旋转 度得到 ,请画出 ;(2)、请以点 为位似中心,画出 的位似三角形 ,使相似比为 .20. 如图,在淮河的右岸边有一高楼,左岸边有一坡度 的山坡 ,点 与点 在同一水平面上, 与 在同一平面内.某数学兴趣小组为了测量楼 的高度,在坡底 处测得楼顶 的仰角为 ,然后沿坡面 上行了 米到达点 处,此时在 处测得楼顶 的仰角为 ,求楼 的高度.(结果保留整数)(参考数 ) 21. 黄山景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高 元,日销量将会减少10件.物价部门规定:销售单价不低于6元,但不能超过12元,设该纪念品的销售单价为 (元),日销量为 (件).(1)、直接写出 与 的函数关系式.(2)、求日销售利润 (元)与销售单价 (元)的函数关系式.并求当 为何值时,日销售利润最大,最大利润是多少?
21. 黄山景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高 元,日销量将会减少10件.物价部门规定:销售单价不低于6元,但不能超过12元,设该纪念品的销售单价为 (元),日销量为 (件).(1)、直接写出 与 的函数关系式.(2)、求日销售利润 (元)与销售单价 (元)的函数关系式.并求当 为何值时,日销售利润最大,最大利润是多少?

