浙江省绍兴市新昌县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 下列图片中是轴对称图形的是( ).A、
 B、
B、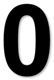 C、
C、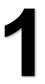 D、
D、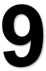 2. 在 中, , ,则 的度数为( ).A、25° B、75° C、55° D、65°3. 如图,点 到 轴的距离是( ).
2. 在 中, , ,则 的度数为( ).A、25° B、75° C、55° D、65°3. 如图,点 到 轴的距离是( ).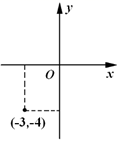 A、-3 B、3 C、-4 D、44. 直线 与 轴的交点坐标为( )A、 B、 C、 D、5. 若 ,则下列各式中成立的是( ).A、 B、 C、 D、6. 下列选项中,可以用来说明命题“如果 ,那么 , ”是假命题的反例是( ).A、 , B、 , C、 , D、 ,7. 已知等腰三角形的周长为13,一条边长为5,则底边长为( ).A、3 B、5 C、5或3 D、4或58. 如图,已知 平分 ,下列所给出的条件不能证明 的是( ).
A、-3 B、3 C、-4 D、44. 直线 与 轴的交点坐标为( )A、 B、 C、 D、5. 若 ,则下列各式中成立的是( ).A、 B、 C、 D、6. 下列选项中,可以用来说明命题“如果 ,那么 , ”是假命题的反例是( ).A、 , B、 , C、 , D、 ,7. 已知等腰三角形的周长为13,一条边长为5,则底边长为( ).A、3 B、5 C、5或3 D、4或58. 如图,已知 平分 ,下列所给出的条件不能证明 的是( ).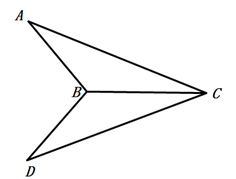 A、 B、 C、 D、9. 为了举行班级晚会,小明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,购买的球拍为x个,那么x的最大值是( )A、7 B、8 C、9 D、1010. 如图,直线 与 相交于点 , 与 轴交于点 , 与 轴交于点 ,与 轴交于点 .下列说法错误的是( ).
A、 B、 C、 D、9. 为了举行班级晚会,小明准备去商店购买20个乒乓球做道具,并买一些乒乓球拍做奖品.已知乒乓球每个1.5元,球拍每个22元.如果购买金额不超过200元,购买的球拍为x个,那么x的最大值是( )A、7 B、8 C、9 D、1010. 如图,直线 与 相交于点 , 与 轴交于点 , 与 轴交于点 ,与 轴交于点 .下列说法错误的是( ).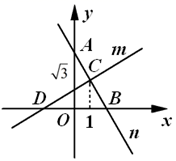 A、 B、 C、 D、直线 的函数表达式为
A、 B、 C、 D、直线 的函数表达式为二、填空题
-
11. 甲的座位在第3列第4行,若记为 ,则乙的座位在第6列第2行,可记为.12. 命题“到线段两端距离相等的点在线段的垂直平分线上”是命题(填“真”或“假”).13. 适合不等式 的最小正整数是.14. 函数 和 的图象相交于点 ,则方程 的解为.15. 如图,已知在 中, 于点 , 为 上一点,且 , ,若 , ,则 .
 16. 已知等边 的边长为3,点 在直线 上,点 在直线 上,且 ,若 ,则 的长为.
16. 已知等边 的边长为3,点 在直线 上,点 在直线 上,且 ,若 ,则 的长为.三、解答题
-
17. 解下列不等式(组)(1)、(2)、18.
如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)
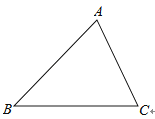 19. 如图,已知点 , , , 在同一条直线上, , , .求证: .
19. 如图,已知点 , , , 在同一条直线上, , , .求证: .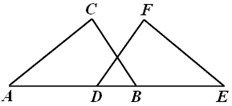 20. 定义:在平面直角坐标系中,一个图形向右平移1个单位再向下平移2个单位称为一个跳步.如:点 一个跳步后对应点 .已知点 , .(1)、求点 , 经过1个跳步后的对应点 , 的坐标.(2)、求直线 经过一个跳步后对应直线的函数表达式.21. 如图,已知在 中, , ,将 沿着 折叠,使点 落在边 上,记为点 .
20. 定义:在平面直角坐标系中,一个图形向右平移1个单位再向下平移2个单位称为一个跳步.如:点 一个跳步后对应点 .已知点 , .(1)、求点 , 经过1个跳步后的对应点 , 的坐标.(2)、求直线 经过一个跳步后对应直线的函数表达式.21. 如图,已知在 中, , ,将 沿着 折叠,使点 落在边 上,记为点 .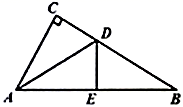 (1)、求证: .(2)、如果 ,求 的面积.22. 直线 与直线 相交于点 .
(1)、求证: .(2)、如果 ,求 的面积.22. 直线 与直线 相交于点 .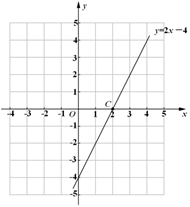 (1)、求 的值,并在图中画出直线 .(2)、根据图象,写出关于 的不等式组 的解集.23. 下表是三种电话计费方式:
(1)、求 的值,并在图中画出直线 .(2)、根据图象,写出关于 的不等式组 的解集.23. 下表是三种电话计费方式:月使用费
(元)
主叫限定时间
(分钟)
主叫超时收费
(元/分钟)
被叫
方式一
18
60
0.2
免费
方式二
28
120
0.2
免费
方式三
48
240
0.2
免费
说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费.
设一个月内主叫通话 分钟( 为正整数).
(1)、当 时,按方式一计费为元;按方式二计费为元.(2)、当 时,是否存在某一时间 ,使方式二与方式三的计费结果相等?若存在,请求出对应的值,若不存在,请说明理由.(3)、当 时,哪一种收费方式最省钱?请说明理由.24. 如图在平面直角坐标系中,点 ,点 是 轴上方的点,且 , 、 分别平分 、 ,过点 作 ,与 的延长线交于点 .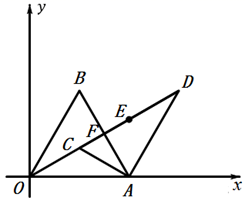 (1)、当 时,求 的长.(2)、求证: .(3)、若 的中点为 ,探究点 横坐标的规律.
(1)、当 时,求 的长.(2)、求证: .(3)、若 的中点为 ,探究点 横坐标的规律.特殊情况探究:①当 时,求出此时点 的横坐标为6,②当 时,求得此时点 的横坐标。
一般情况探究:③当 时,点 横坐标的规律是什么?并证明这个规律.