安徽省阜阳市阜南县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 下列计算正确的是( )A、2a+5b=10ab B、(﹣ab)2=a2b C、2a6÷a3=2a3 D、a2•a4=a83. 若双曲线y= 在每一个象限内,y随x的增大而减小,则k的取值范围是( )A、k<3 B、k≥3 C、k>3 D、k≠34. 对于函数 ,下列结论错误的是( )A、图象顶点是 B、图象开口向上 C、图象关于直线 对称 D、图象最大值为﹣95. 反比例函数图象的一支如图所示, 的面积为2,则该函数的解析式是( )
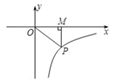 A、 B、 C、 D、6. 如图,在平行四边形ABCD中,E为CD上一点,连接AE , BD , 且AE , BD交于点F , : :25,则DE: =( )
A、 B、 C、 D、6. 如图,在平行四边形ABCD中,E为CD上一点,连接AE , BD , 且AE , BD交于点F , : :25,则DE: =( )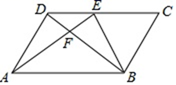 A、2:5 B、3:2 C、2:3 D、5:37. 直角三角形两直角边之和为定值,其面积 与一直角边 之间的函数关系大致图象是下列中的( )A、
A、2:5 B、3:2 C、2:3 D、5:37. 直角三角形两直角边之和为定值,其面积 与一直角边 之间的函数关系大致图象是下列中的( )A、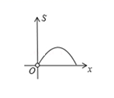 B、
B、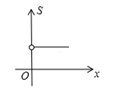 C、
C、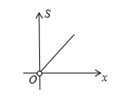 D、
D、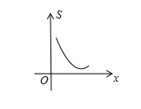 8. 如图,AG:GD=4:1,BD:DC=2:3,则 AE:EC 的值是( )
8. 如图,AG:GD=4:1,BD:DC=2:3,则 AE:EC 的值是( )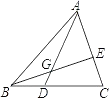 A、3:2 B、4:3 C、6:5 D、8:59. 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(1,0),对称轴是直线x=-1,则ax2+bx+c=0的解是( )
A、3:2 B、4:3 C、6:5 D、8:59. 如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(1,0),对称轴是直线x=-1,则ax2+bx+c=0的解是( )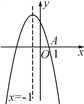 A、x1=-3,x2=1 B、x1=3,x2=1 C、x=-3 D、x=-210. 抛物线 ( )的部分图象如图所示,与 轴的一个交点坐标为 ,抛物线的对称轴是 ,下列结论是:① ;② ;③方程 有两个不相等的实数根;④ ;⑤若点 在该抛物线上,则 ,其中正确的个数有( )
A、x1=-3,x2=1 B、x1=3,x2=1 C、x=-3 D、x=-210. 抛物线 ( )的部分图象如图所示,与 轴的一个交点坐标为 ,抛物线的对称轴是 ,下列结论是:① ;② ;③方程 有两个不相等的实数根;④ ;⑤若点 在该抛物线上,则 ,其中正确的个数有( )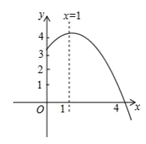 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
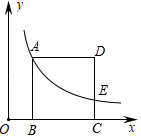
11. 若x:y=5:2,则(x+y):y的值是12. 如果抛物线 经过原点,那么m=.13. 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= (k≠0)在第一象限的图象经过顶点A(m,2)和CD边上的点E(n, ),则点D的坐标是 .
 14. 如图1,点M,N,P,Q分别在矩形ABCD的边AB,BC,CD,DA上,我们称四边形MNPQ是矩形ABCD的内接四边形.已知矩形ABCD,AB=2BC=6,若它的内接四边形MNPQ也是矩形,且相邻两边的比为3:1,则AM= .
14. 如图1,点M,N,P,Q分别在矩形ABCD的边AB,BC,CD,DA上,我们称四边形MNPQ是矩形ABCD的内接四边形.已知矩形ABCD,AB=2BC=6,若它的内接四边形MNPQ也是矩形,且相邻两边的比为3:1,则AM= .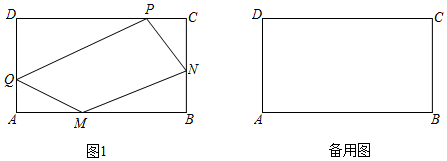
三、解答题
-
15. 计算: +20﹣|﹣3|+(﹣ )﹣1 .16. 阅读材料,解答问题:
观察下列方程:① ;② ;③ ;…;
(1)、按此规律写出关于x的第4个方程为 , 第n个方程为;(2)、直接写出第n个方程的解,并检验此解是否符合题意.17. 如图,DC∥EF∥GH∥AB,AB=12,CD=6,DE:EG:GA=3:4:5.求EF和GH的长.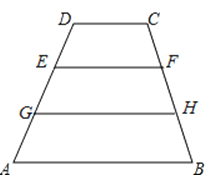 18. 如图,一次函数 的图象与反比例函数 的图象交于 ,B 两点.
18. 如图,一次函数 的图象与反比例函数 的图象交于 ,B 两点.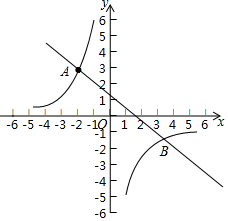 (1)、求一次函数与反比例函数的解析式;(2)、结合图形,直接写出一次函数大于反比例函数时自变量x的取值范围.19. 已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD.
(1)、求一次函数与反比例函数的解析式;(2)、结合图形,直接写出一次函数大于反比例函数时自变量x的取值范围.19. 已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE•GD.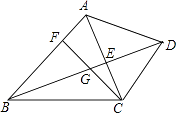 (1)、求证:∠ACF=∠ABD;(2)、连接EF,求证:EF•CG=EG•CB.20. 若二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如表:
(1)、求证:∠ACF=∠ABD;(2)、连接EF,求证:EF•CG=EG•CB.20. 若二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如表:x
…
-2
-1
0
1
2
…
y
…
0
-2
-2
0
4
…
(1)、求该二次函数的表达式;(2)、当y≥4时,求自变量x的取值范围.21. 随着技术的发展进步,某公司2018年采用的新型原料生产产品.这种新型原料的用量y(吨)与月份x之间的关系如图1所示,每吨新型原料所生产的产品的售价z(万元)与月份x之间的关系如图2所示.已知将每吨这种新型原料加工成的产品的成本为20万元.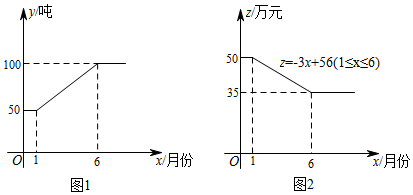 (1)、求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;(2)、若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?22. 如图1,我们已经学过:点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1 , S2 , 如果 ,那么称直线l为该图形的黄金分割线.
(1)、求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;(2)、若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?22. 如图1,我们已经学过:点C将线段AB分成两部分,如果 ,那么称点C为线段AB的黄金分割点.某校的数学拓展性课程班,在进行知识拓展时,张老师由黄金分割点拓展到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1 , S2 , 如果 ,那么称直线l为该图形的黄金分割线.如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D.
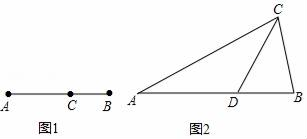 (1)、证明点D是AB边上的黄金分割点;(2)、证明直线CD是△ABC的黄金分割线.23. 如图,在 中, 为边 的中点, 为线段 上一点,联结 并延长交边 于点 ,过点 作 的平分线,交射线 于点 .设 .
(1)、证明点D是AB边上的黄金分割点;(2)、证明直线CD是△ABC的黄金分割线.23. 如图,在 中, 为边 的中点, 为线段 上一点,联结 并延长交边 于点 ,过点 作 的平分线,交射线 于点 .设 .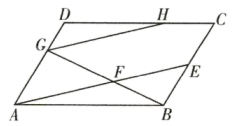 (1)、当 时,求 的值;(2)、设 ,求关于 的函数解析式,并写出x的取值范围;(3)、当 时,求 的值.
(1)、当 时,求 的值;(2)、设 ,求关于 的函数解析式,并写出x的取值范围;(3)、当 时,求 的值.