安徽省滁州市全椒县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若α为锐角,且 ,则α等于( )A、80° B、70° C、60° D、50°3. 若 . 则下列式子正确的是( )A、 B、 C、 D、4. 以 为顶点的二次函数是( )A、 B、 C、 D、5. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
2. 若α为锐角,且 ,则α等于( )A、80° B、70° C、60° D、50°3. 若 . 则下列式子正确的是( )A、 B、 C、 D、4. 以 为顶点的二次函数是( )A、 B、 C、 D、5. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( ) A、3:4 B、9:16 C、9:1 D、3:16. 如图,二次函数 的最大值为3,一元二次方程 有实数根,则 的取值范围是( )
A、3:4 B、9:16 C、9:1 D、3:16. 如图,二次函数 的最大值为3,一元二次方程 有实数根,则 的取值范围是( ) A、m≥3 B、m≥-3 C、m≤3 D、m≤-37. 按如图所示的方法折纸,下面结论正确的个数( )
A、m≥3 B、m≥-3 C、m≤3 D、m≤-37. 按如图所示的方法折纸,下面结论正确的个数( )①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.
 A、1 个 B、2 个 C、3 个 D、4 个8. 如果某人沿坡度为3:4的斜坡前进10m,那么他所在的位置比原来的位置升高了( )A、6m B、8m C、10m D、12m9. 如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )
A、1 个 B、2 个 C、3 个 D、4 个8. 如果某人沿坡度为3:4的斜坡前进10m,那么他所在的位置比原来的位置升高了( )A、6m B、8m C、10m D、12m9. 如图,点A,B,C均在⊙O上,当∠OBC=40°时,∠A的度数是( )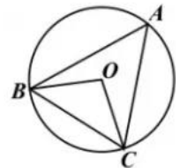 A、50° B、55° C、60° D、65°10. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )
A、50° B、55° C、60° D、65°10. 图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是( )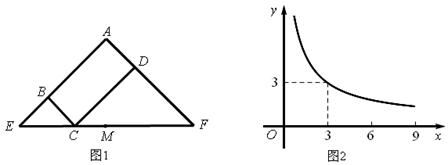 A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。
A、当x=3时,EC<EM B、当y=9时,EC>EM C、当x增大时,EC·CF的值增大。 D、当y增大时,BE·DF的值不变。二、填空题
-
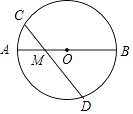
11. 已知 , 是抛物线 上两点,该抛物线的解析式是 .12. 在比例尺为1:40000的地图上,某条道路的长为7cm,则该道路的实际长度是 km.13. 如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C,D两点.若∠CMA=45°,则弦CD的长为 .
 14. 如图,在直角坐标系中,点 ,点 ,过点 的直线 垂直于线段 ,点 是直线 上在第一象限内的一动点,过点 作 轴,垂足为 ,把 沿 翻折 ,使点 落在点 处,若以 , , 为顶点的三角形与△ABP相似,则满足此条件的点 的坐标为 .
14. 如图,在直角坐标系中,点 ,点 ,过点 的直线 垂直于线段 ,点 是直线 上在第一象限内的一动点,过点 作 轴,垂足为 ,把 沿 翻折 ,使点 落在点 处,若以 , , 为顶点的三角形与△ABP相似,则满足此条件的点 的坐标为 .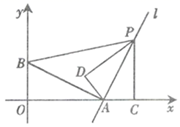
三、解答题
-
15. 计算: .16. 已知 是二次函数,且函数图象有最高点.(1)、求 的值;(2)、当 为何值时, 随 的增大而减少.17. 如图是某区域的平面示意图,码头A在观测站B的正东方向,码头A的北偏西 方向上有一小岛C , 小岛C在观测站B的北偏西 方向上,码头A到小岛C的距离AC为10海里.
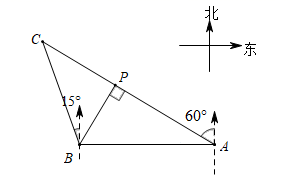 (1)、填空: 度, 度;(2)、求观测站B到AC的距离BP(结果保留根号).18. 如图,锐角三角形 中, , 分别是 , 边上的高,垂足为 , .
(1)、填空: 度, 度;(2)、求观测站B到AC的距离BP(结果保留根号).18. 如图,锐角三角形 中, , 分别是 , 边上的高,垂足为 , .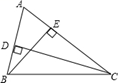 (1)、证明: .(2)、若将 , 连接起来,则 与 能相似吗?说说你的理由.19. 如图, 的直径 垂直于弦 ,垂足为 , 为 延长线上一点,且 .
(1)、证明: .(2)、若将 , 连接起来,则 与 能相似吗?说说你的理由.19. 如图, 的直径 垂直于弦 ,垂足为 , 为 延长线上一点,且 .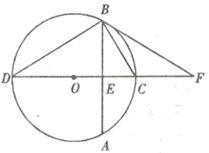 (1)、求证: 为 的切线;(2)、若 , ,求 的半径.20. 如图,已知 的三个顶点的坐标分别为 、 、 , 是 的边 上一点.
(1)、求证: 为 的切线;(2)、若 , ,求 的半径.20. 如图,已知 的三个顶点的坐标分别为 、 、 , 是 的边 上一点.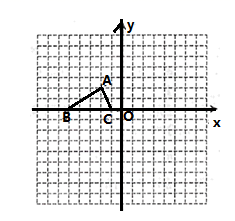 (1)、将 绕原点 逆时针旋转 得到 ,请在网格中画出 ;(2)、将 沿一定的方向平移后,点 的对应点为 ,请在网格中画出上述平移后的 ,并写出点 的坐标(3)、若以点 为位似中心,作 与 成 的位似,则与点 对应的点 位似坐标为(不用作图,直接写出结果).21. 直线y=kx+b与反比例函数 (x>0)的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D.
(1)、将 绕原点 逆时针旋转 得到 ,请在网格中画出 ;(2)、将 沿一定的方向平移后,点 的对应点为 ,请在网格中画出上述平移后的 ,并写出点 的坐标(3)、若以点 为位似中心,作 与 成 的位似,则与点 对应的点 位似坐标为(不用作图,直接写出结果).21. 直线y=kx+b与反比例函数 (x>0)的图象分别交于点A(m,4)和点B(8,n),与坐标轴分别交于点C和点D. (1)、求直线AB的解析式;(2)、观察图象,当x>0时,直接写出 的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.22. 东坡商贸公司购进某种水果成本为20元/ ,经过市场调研发现,这种水果在未来48天的销售单价 (元/ )与时间 (天)之间的函数关系式 , 为整数,且其日销售量 ( )与时间 (天)的关系如下表:
(1)、求直线AB的解析式;(2)、观察图象,当x>0时,直接写出 的解集;(3)、若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.22. 东坡商贸公司购进某种水果成本为20元/ ,经过市场调研发现,这种水果在未来48天的销售单价 (元/ )与时间 (天)之间的函数关系式 , 为整数,且其日销售量 ( )与时间 (天)的关系如下表:时间 (天)
1
3
6
10
20
…
日销售量 ( )
118
114
108
100
80
…
(1)、已知 与 之间的变化符合一次函数关系,试求在第30天的日销售量;(2)、哪一天的销售利润最大?最大日销售利润为多少?23. 在等腰直角三角形 中, , ,点 在斜边 上( ),作 ,且 ,连接 ,如图(1).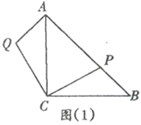 (1)、求证: ;(2)、延长 至点 ,使得 , 与 交于点 .如图(2).
(1)、求证: ;(2)、延长 至点 ,使得 , 与 交于点 .如图(2).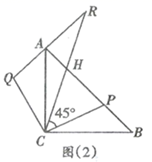
①求证: ;
②求证: .