浙江省绍兴市柯桥区2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-11-02 类型：期末考试

进入出卷网下载

一、选择题

1. 柯桥区作为浙江省试点先行区，四年前就开始实行垃圾分类，以下是几种垃圾分类的图标，其中哪个几何图标是轴对称图形（）

A、 B、 C、 D、

查看试题解析
2. 以下列各组线段长为边，不能组成三角形的是（）

A、8cm，7cm，13cm B、6cm，6cm，12cm C、5cm，5cm，2cm D、10cm，15cm，17cm

查看试题解析
3. 若 $x > y$ ，则下列式子错误的是（）.

A、 $x - 3 > y - 3$ B、 $\frac{x}{3} > \frac{y}{3}$ C、 $- 2 x < - 2 y$ D、 $3 - x > 3 - y$

查看试题解析
4. 用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）

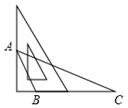A、 B、 C、 D、

查看试题解析
5. 笛卡尔是法国著名的数学家，他首先提出并创建了坐标的思想，引入坐标和变量的概念，平面直角坐标系很好地体现了下列哪一种数学思想？（）

A、分类讨论 B、类比 C、数形结合 D、统计

查看试题解析
6. 已知点 $(1 ， m)$ 和点 $(3 ， n)$ 是一次函数 $y = - 2 x + h$ 图象上的两个点，则 $m$ 与 $n$ 的大小关系是（）

A、 $m > n$ B、 $m < n$ C、 $m = n$ D、以上都不对

查看试题解析
7. 如图，点 $D$ ， $E$ 在 $△ A B C$ 边上，沿 $D E$ 将 $△ A D E$ 翻折，点 $A$ 的对应点为点 $A^{'}$ ， $∠ A^{'} E C = 40 °$ ， $∠ A^{'} D B = 110 °$ ，则 $∠ A$ 等于（）

A、 $30 °$ B、 $35 °$ C、 $60 °$ D、 $70 °$

查看试题解析
8. 若点 $A (2 ， - 3)$ ， $B (4 ， 3)$ ， $C (5 ， a)$ 在同一条直线上，则a的值是（）

A、6或-6 B、6 C、-6 D、6或3

查看试题解析
9. 下列推理正确的是（）

A、∵等腰三角形是轴对称图形，又∵等腰三角形是等边三角形，∴等边三角形是轴对称图形 B、∵轴对称图形是等腰三角形，又∵等边三角形是等腰三角形，∴等边三角形是轴对称图形 C、∵等腰三角形是轴对称图形，又∵等边三角形是等腰三角形，∴等边三角形是轴对称图形 D、∵等边三角形是等腰三角形，又∵等边三角形是轴对称图形，∴等腰三角形是轴对称图形

查看试题解析
10. 如图，直线y＝kx+b与y＝mx+n分别交x轴于点A（﹣1，0），B（4，0），则函数y＝（kx+b）（mx+n）中，则不等式 $(k x + b) (m x + n) > 0$ 的解集为（）

A、x＞2 B、0＜x＜4 C、﹣1＜x＜4 D、x＜﹣1 或 x＞4

查看试题解析

二、填空题

11. 为说明命题“如果a＞b，那么 $\frac{1}{a} > \frac{1}{b}$ ”是假命题，你举出的反例是．

查看试题解析
12. $△ ABC$ ≌ $△ DEF$ ，且 $△ ABC$ 的周长为 $12 ，若 AC = 3 ， EF = 4 ， AB =$ .

查看试题解析
13. 将直线y＝-2x＋3向下平移5个单位，得到直线

查看试题解析
14. 如图所示，AB交CD于O点，OA=OB，请你添加一个条件，使得△AOC≌△BOD，你添加的条件是。

查看试题解析
15. 定义：对于一次函数 $y = k x + b$ ，我们把点 $(b ， k)$ 称为这个一次函数的伴随点.已知一次函数 $y = - 4 x + m$ 的伴随点在它的图象上，则 $m =$ .

查看试题解析
16. 小敏从学校步行回家，突然想起忘记带家庭作业，他又返回了学校，拿了家庭作业，然后步行回家.图表显示了不同时间他离家的距离.问他一共走了米路才到家.

查看试题解析
17. 八年级师生组织捐款，共捐得2100元，这个年级有教师35名，14个教学班.各班学生人数都相同且多于30人，不超过40人.若平均每人捐款的金额恰好是整数元，则平均每人捐款元.

查看试题解析
18. 《九章算术》提供了许多整勾股数，如 $(3 ， 4 ， 5)$ ， $(5 ， 12 ， 13)$ ， $(7 ， 24 ， 25)$ ， $(8 ， 15 ， 17)$ 等等，并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究，得到如下规律：若 $m$ 是大于1的奇数，把它平方后拆成相邻的两个整数，那么 $m$ 与这两个整数构成一组勾股数；若 $m$ 是大于2的偶数，把它除以2后再平方，然后把这个平方数分别减1，加l得到两个整数，那么 $m$ 与这两个整数构成一组勾股数.由上述方法得到的勾股数称为“由 $m$ 生成的勾股数”.若“由9生成的勾股数”的“弦数“记为 $A$ ，“由20生成的勾股数”的“弦数“记为 $B$ ，则 $A + B =$ .

查看试题解析
19. $m$ 为实数，由所有位于第二象限内的点 $P (m ， m + 1)$ 组成的图象与两坐标轴围成的封闭几何图形的周长是.

查看试题解析
20. 在 $R t △ A B C$ 中， $∠ A = 90 °$ ，其中一个锐角为 $60 °$ ， $B C = 2 \sqrt{3}$ ，点 $P$ 在直线 $A C$ 上（不与 $A$ ， $C$ 两点重合），当 $∠ A B P = 30 °$ 时， $C P$ 的长为.

查看试题解析

三、解答题

21. 解不等式组 ${\begin{cases} x - 1 < 2 \\ \frac{x + 2}{3} \geq - 1 \end{cases}$ ，并把解集表示在数轴上.

查看试题解析
22. 如图，在等边△ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，

(1)、求∠F的度数；

(2)、若CD=5，求DF的长．

查看试题解析
23. $△ ABC$ 在平面直角坐标系中的位置如图.

（ 1 ）作出 $△ ABC$ 关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出 $△ A_{1} B_{1} C_{1}$ 各顶点坐标；

（ 2 ）将 $△ ABC$ 向右平移 $6$ 个单位，作出平移后的 $△ A_{2} B_{2} C_{2}$ ，并写出 $△ A_{2} B_{2} C_{2}$ 各顶点的坐标.

查看试题解析
24. 如图，在△ABC中，AB=AC，D是三角形内一点，连接AD，BD，CD，∠BDC=90°，∠DBC=45°.

(1)、求证：∠BAD=∠CAD；

(2)、求∠ADB的度数.

查看试题解析
25. 某厂家在甲、乙两家商场销售同一商品所获得的利润分别为 $y_{甲}$ ， $y_{乙}$ （单位：元）， $y_{甲}$ ， $y_{乙}$ 与销售数量x（单位：件）的函数关系如图所示，试根据图象解决下列问题：

(1)、分别求出 $y_{甲}$ ， $y_{乙}$ 关于x的函数关系式；

(2)、现厂家分配该商品800件给甲商场，400件给乙商场，当甲、乙商场售完这批商品后，厂家可获得的总利润是多少元？

查看试题解析
26. 小明在学习过程中，对教材中的一个有趣问题做如下探究：

(1)、（习题回顾）已知：如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A E$ 是角平分线， $C D$ 是高， $A E$ 、 $C D$ 相交于点 $F$ .求证： $∠ C F E = ∠ C E F$ ；

(2)、（变式思考）如图2，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是 $A B$ 边上的高，若 $△ A B C$ 的外角 $∠ B A G$ 的平分线交 $C D$ 的延长线于点 $F$ ，其反向延长线与 $B C$ 边的延长线交于点 $E$ ，则 $∠ C F E$ 与 $∠ C E F$ 还相等吗？说明理由；

(3)、（探究延伸）如图3，在 $△ A B C$ 中， $A B$ 上存在一点 $D$ ，使得 $∠ A C D = ∠ B$ ， $∠ B A C$ 的平分线 $A E$ 交 $C D$ 于点 $F$ . $△ A B C$ 的外角 $∠ B A G$ 的平分线所在直线 $M N$ 与 $B C$ 的延长线交于点 $M$ .直接写出 $∠ M$ 与 $∠ C F E$ 的数量关系.

查看试题解析
27. 如图1，在平面直角坐标系中，直线 $y = \frac{1}{2} x + 4$ 经过点 $A (\frac{10}{3} ， m)$ ，与 $x$ 轴， $y$ 轴分别交于 $B$ ， $C$ 两点，点 $D (0 ， - 1)$ ， $P (t ， 0) (t > - 8)$

(1)、求 $m$ 的值和直线 $A D$ 的函数表达式；

(2)、连结 $C P$ ，当 $△ B P C$ 是等腰三角形时，求 $t$ 的值；

(3)、若 $t = - 4$ ，点 $M$ ， $N$ 分别在线段 $A B$ ，线段 $A D$ 上，当 $△ P M N$ 是等腰直角三角形且 $∠ M P N = 45 °$ 时，则 $△ P M N$ 的面积是.

查看试题解析