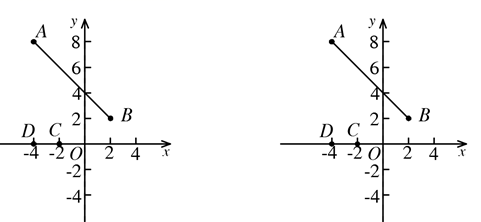浙江省宁波市七中教育集团2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,点P(3,﹣2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是 ( )A、3cm B、4cm C、7cm D、11cm3. 下列图形中的曲线不表示y是x的函数的是( )A、
 B、
B、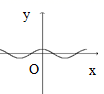 C、
C、 D、
D、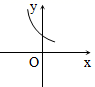 4. 已知不等式x+1≥0,其解集在数轴上表示正确的是( )A、
4. 已知不等式x+1≥0,其解集在数轴上表示正确的是( )A、 B、
B、 C、
C、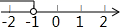 D、
D、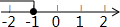 5. 已知点 和 在一次函数 的图象上,则 与 的大小关系是( )A、 B、 C、 D、6. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:
5. 已知点 和 在一次函数 的图象上,则 与 的大小关系是( )A、 B、 C、 D、6. 将一组数 ,2, ,2 , ,…,2 ,按下列方式进行排列:,2, ,2 , ;
2 , ,4,3 ,2 ;
…
若2的位置记为(1,2),2 的位置记为(2,1),则 这个数的位置记为( )
A、(5,4) B、(4,4) C、(4,5) D、(3,5)7. 要说明命题“若 ,则 ”是假命题,能举的一个反例是A、 , B、 , C、 , D、 ,8. 如图,△ABC的面积为8cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )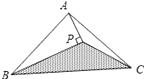 A、2cm2 B、3cm2 C、4cm2 D、5cm29. 已知 ,现把小棒依次摆放在两射线 之间,并使小棒在两射线上,从 开始,用等长的小棒依次向右摆放,其中 为第1根小棒,且 ,若只能摆放9根小棒,则 的度数可以是( )
A、2cm2 B、3cm2 C、4cm2 D、5cm29. 已知 ,现把小棒依次摆放在两射线 之间,并使小棒在两射线上,从 开始,用等长的小棒依次向右摆放,其中 为第1根小棒,且 ,若只能摆放9根小棒,则 的度数可以是( )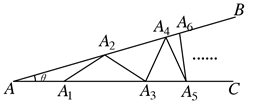 A、6° B、7° C、8° D、9°10. 如图,点 的坐标为(3,4), 轴于点 , 是线段 上一点,且 ,点 从原点 出发,沿 轴正方向运动, 与直线 交于 ,则 的面积( )
A、6° B、7° C、8° D、9°10. 如图,点 的坐标为(3,4), 轴于点 , 是线段 上一点,且 ,点 从原点 出发,沿 轴正方向运动, 与直线 交于 ,则 的面积( )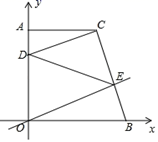 A、逐渐变大 B、先变大后变小 C、逐渐变小 D、始终不变
A、逐渐变大 B、先变大后变小 C、逐渐变小 D、始终不变二、填空题
-
11. 二次根式 中,x的取值范围是 .12. 点A(﹣3,2)关于y轴的对称点坐标是 .
13. 一次函数y=(2m-6)x+5中,y随x的增大而减小,则m的取值范围是 .14. 若点 , 在正比例函数图象上,请写出正比例函数的表达式.15. 如图,在 中, , ,点 是 边上的动点,设 ,当 为直角三角形时, 的值是.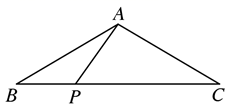 16. 如图,若△ABC≌△ADE,且∠B=65°,则∠BAD=.
16. 如图,若△ABC≌△ADE,且∠B=65°,则∠BAD=. 17. 如图,长方形两边长 ,两顶点 分别在 轴的正半轴和 轴的正半轴上运动,则顶点 到原点 的距离最大值是.
17. 如图,长方形两边长 ,两顶点 分别在 轴的正半轴和 轴的正半轴上运动,则顶点 到原点 的距离最大值是.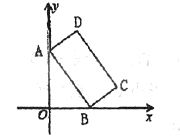 18. 如图,矩形纸片 , , ,点 在 边上,将 沿 折叠,点 落在 处, 分别交 于点 ,且 ,则 长为
18. 如图,矩形纸片 , , ,点 在 边上,将 沿 折叠,点 落在 处, 分别交 于点 ,且 ,则 长为
三、解答题
-
19.(1)、计算:(2)、解不等式组20. 如图:已知直线 经过点 , .
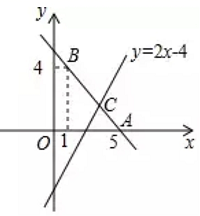 (1)、求直线 的解析式;(2)、若直线 与直线 相交于点 ,求点 的坐标;(3)、根据图象,直接写出关于 的不等式 的解集.21. 小慧根据学习函数的经验,对函数 图象与性质进行了探究,下面是小慧的探究过程,请补充完整:
(1)、求直线 的解析式;(2)、若直线 与直线 相交于点 ,求点 的坐标;(3)、根据图象,直接写出关于 的不等式 的解集.21. 小慧根据学习函数的经验,对函数 图象与性质进行了探究,下面是小慧的探究过程,请补充完整: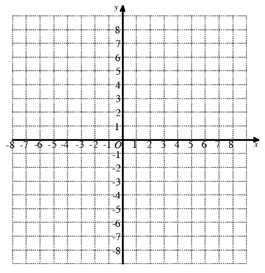 (1)、若 , 为该函数图象上不同的两点,则 , 该函数的最小值为.(2)、请在坐标系中画出直线 与函数 的图象并写出当 时 的取值范围是.22. 如图:等边 中, 上,且 , 相交于点 ,连接 .
(1)、若 , 为该函数图象上不同的两点,则 , 该函数的最小值为.(2)、请在坐标系中画出直线 与函数 的图象并写出当 时 的取值范围是.22. 如图:等边 中, 上,且 , 相交于点 ,连接 . (1)、证明 .(2)、若 ,证明 是等腰三角形.23. 如图, , , 为 中点
(1)、证明 .(2)、若 ,证明 是等腰三角形.23. 如图, , , 为 中点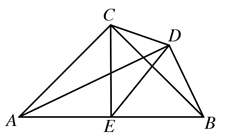 (1)、若 ,求 的周长和面积.(2)、若 ,求 的面积.24. 已知:如图,在平面直角坐标系中, 为坐标原点, , ,过点 画 交直线 于 (即点 的纵坐标始终为 ),连接 .
(1)、若 ,求 的周长和面积.(2)、若 ,求 的面积.24. 已知:如图,在平面直角坐标系中, 为坐标原点, , ,过点 画 交直线 于 (即点 的纵坐标始终为 ),连接 . (1)、求 的长.(2)、若 为等腰直角三角形,求 的值.(3)、在(2)的条件下求 所在直线的表达式.(4)、用 的代数式表示 的面积.
(1)、求 的长.(2)、若 为等腰直角三角形,求 的值.(3)、在(2)的条件下求 所在直线的表达式.(4)、用 的代数式表示 的面积.