浙江省宁波市江北区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边长分别为8和4,则第三边长可能是( )A、3 B、4 C、8 D、123. 如果 ,下列各式中不正确的是( )A、 B、 C、 D、4. 在 和 中,已知 , ,添加下列条件中的一个,不能使 一定成立的是( )A、 B、 C、 D、5. 在平面直角坐标系中,点 关于 轴的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 把函数 的图象向上平移2个单位,则下列各坐标所表示的点中,在平移后的直线上的是( )A、 B、 C、 D、7. 如图, 中, 垂直平分 ,垂足为 , , 的周长为13,那么 的周长为( )
2. 已知三角形的两边长分别为8和4,则第三边长可能是( )A、3 B、4 C、8 D、123. 如果 ,下列各式中不正确的是( )A、 B、 C、 D、4. 在 和 中,已知 , ,添加下列条件中的一个,不能使 一定成立的是( )A、 B、 C、 D、5. 在平面直角坐标系中,点 关于 轴的对称点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 把函数 的图象向上平移2个单位,则下列各坐标所表示的点中,在平移后的直线上的是( )A、 B、 C、 D、7. 如图, 中, 垂直平分 ,垂足为 , , 的周长为13,那么 的周长为( ) A、10 B、13 C、16 D、198. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )
A、10 B、13 C、16 D、198. 如图,将一张三角形纸片 的一角折叠,使点 落在 处的 处,折痕为 .如果 , , ,那么下列式子中正确的是( )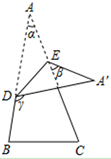 A、 B、 C、 D、9. 关于x的不等式组 的解集为 ,那么a的取值范围为( )A、 B、 C、 D、10. 如图,在等腰 中, ,点 在 轴正半轴上,点 在第一象限,以 为斜边向右侧作等腰 ,则直线 的函数表达式为( )
A、 B、 C、 D、9. 关于x的不等式组 的解集为 ,那么a的取值范围为( )A、 B、 C、 D、10. 如图,在等腰 中, ,点 在 轴正半轴上,点 在第一象限,以 为斜边向右侧作等腰 ,则直线 的函数表达式为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 的 与 的2倍的和是非正数,用不等式表示为.12. 将“对顶角相等”改写为“如果...那么...”的形式,可写为.13. 已知 ,则 点到 轴的距离为.14. 若一次函数 的图象不经过第三象限,则 的取值范围是.15. 等腰三角形的一边长为2,周长为5,那么它的腰长为.16. 已知点 , 是一次函数 图象上的两点,当 时, (填“ ”“ ”或“ ”)17. 如图,在平面直角坐标系中,直线 分别与 轴、 轴相交于 、 ,线段 的垂直平分线交 轴于点 ,垂足为 ,则点 的坐标为.
 18. 如图,在等边 中, ,点 在 上,且 ,点 是 上一动点,连结 ,将线段 绕点 逆时针旋转 得到线段 .要使点 恰好落在 上,则 的长是.
18. 如图,在等边 中, ,点 在 上,且 ,点 是 上一动点,连结 ,将线段 绕点 逆时针旋转 得到线段 .要使点 恰好落在 上,则 的长是.
三、解答题
-
19. 解下列不等式(组)(1)、(2)、20.
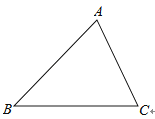
如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)
 21. 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
21. 某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.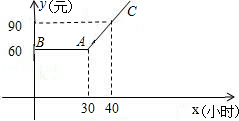 (1)、当x≥30,求y与x之间的函数关系式;(2)、若小李4月份上网20小时,他应付多少元的上网费用?(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?22. 如图, 是 平分线上的一点,若 ,
(1)、当x≥30,求y与x之间的函数关系式;(2)、若小李4月份上网20小时,他应付多少元的上网费用?(3)、若小李5月份上网费用为75元,则他在该月份的上网时间是多少?22. 如图, 是 平分线上的一点,若 ,证明:
 23. 如图,在平面直角坐标系xOy中,一次函数 的图象经过点A( , ),且与正比例函数 的图象交于点B( , ).
23. 如图,在平面直角坐标系xOy中,一次函数 的图象经过点A( , ),且与正比例函数 的图象交于点B( , ). (1)、求 的值及一次函数 的解析式;(2)、若一次函数 的图象与x轴交于点C,且正比例函数 的图象向下平移m(m>0)个单
(1)、求 的值及一次函数 的解析式;(2)、若一次函数 的图象与x轴交于点C,且正比例函数 的图象向下平移m(m>0)个单位长度后经过点C,求m的值;
(3)、直接写出关于x的不等式 的解集.24. 如图1,已知直线 的同侧有两个点 、 ,在直线 上找一点 ,使 点到 、 两点的距离之和最短的问题,可以通过轴对称来确定,即作出其中一点关于直线 的对称点,对称点与另一点的连线与直线 的交点就是所要找的点,通过这种方法可以求解很多问题. (1)、如图2,在平面直角坐标系内,点 的坐标为 ,点 的坐标为 ,动点 在 轴上,求 的最小值;(2)、如图3,在锐角三角形 中, , , 的角平分线交 于点 , 、 分别是 和 上的动点,则 的最小值为.(3)、如图4, , , ,点 , 分别是射线 , 上的动点,则 的最小值为.
(1)、如图2,在平面直角坐标系内,点 的坐标为 ,点 的坐标为 ,动点 在 轴上,求 的最小值;(2)、如图3,在锐角三角形 中, , , 的角平分线交 于点 , 、 分别是 和 上的动点,则 的最小值为.(3)、如图4, , , ,点 , 分别是射线 , 上的动点,则 的最小值为.