浙江省宁波市海曙区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 下列是世界各国银行的图标,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个正比例函数的图象过点(2,﹣3),它的表达式为( )
2. 一个正比例函数的图象过点(2,﹣3),它的表达式为( )
A、 B、 C、 D、3. 已知等腰三角形ABC中,腰AB=8,底BC=5,则这个三角形的周长为( )A、21 B、20 C、19 D、184. 已知关于x的不等式2x-m>-3的解集如图所示,则m的取值为( ) A、2 B、1 C、0 D、-15. 一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC的度数为( )
A、2 B、1 C、0 D、-15. 一副透明的三角板,如图叠放,直角三角板的斜边AB、CE相交于点D,则∠BDC的度数为( )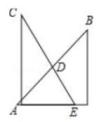 A、60° B、45° C、75° D、90°6. 如图,△ABC≌△AEF且点F在BC上,若AB=AE,∠B=∠E,则下列结论错误的是( )
A、60° B、45° C、75° D、90°6. 如图,△ABC≌△AEF且点F在BC上,若AB=AE,∠B=∠E,则下列结论错误的是( )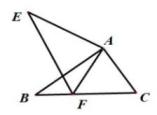 A、AC=AF B、∠AFE=∠BFE C、EF=BC D、∠EAB=∠FAC7. 能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )A、120°,60° B、95°,105° C、30°,60° D、90°,90°8. 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?( )
A、AC=AF B、∠AFE=∠BFE C、EF=BC D、∠EAB=∠FAC7. 能说明命题“如果两个角互补,那么这两个角一个是锐角,另一个是钝角”为假命题的两个角是( )A、120°,60° B、95°,105° C、30°,60° D、90°,90°8. 如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?( )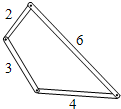 A、5 B、6 C、7 D、109. 如图的 中, ,且 为 上一点.今打算在 上找一点 ,在 上找一点 ,使得 与 全等,以下是甲、乙两人的作法:
A、5 B、6 C、7 D、109. 如图的 中, ,且 为 上一点.今打算在 上找一点 ,在 上找一点 ,使得 与 全等,以下是甲、乙两人的作法:(甲)连接 ,作 的中垂线分别交 、 于 点、 点,则 、 两点即为所求
(乙)过 作与 平行的直线交 于 点,过 作与 平行的直线交 于 点,则 、 两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
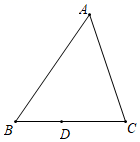 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确10. 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx﹣2的解集是( ).
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确10. 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx﹣2的解集是( ).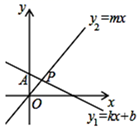 A、 B、 C、 D、1<x<2
A、 B、 C、 D、1<x<2二、填空题
-
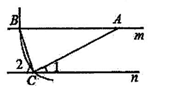
11. 6与x的2倍的和是负数,用不等式表示为。12. 将点P(-1,2)向左平移2个单位,再向上平移1个单位所得的对应点的坐标为。13. 已知CD是Rt△ABC的斜边AB上的中线,若∠A=35°,则∠BCD=.14. 已知点A(-3,m)与点B(2,n)是直线y=- x+b上的两点,则m与n的大小关系是.15. 如图,直线m∥n,以直线m上的点A为圆心,适当长为半径画弧,分别交直线m,n于点B、C,连接AC、BC,若∠1=30°,则∠2= .
 16. 已知点A(4,3),AB∥y轴,且AB=3,则B点的坐标为.17. 一次生活常识知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分,小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对了道题。18. 如图,10个边长为1的正方形摆放在平面直角坐标系中,经过A(1,0)点的一条直线l将这10个正方形分成面积相等的两部分,则该直线的解析式为.
16. 已知点A(4,3),AB∥y轴,且AB=3,则B点的坐标为.17. 一次生活常识知识竞赛一共有20道题,答对一题得5分,不答得0分,答错扣2分,小聪有1道题没答,竞赛成绩超过80分,则小聪至少答对了道题。18. 如图,10个边长为1的正方形摆放在平面直角坐标系中,经过A(1,0)点的一条直线l将这10个正方形分成面积相等的两部分,则该直线的解析式为.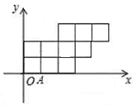
三、解答题
-
19. 解不等式组 ,并把它的解集在数轴上表示出来。20. 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,﹣3),B(5,﹣1),C(1,3),结合所给的平面直角坐标系,解答下列问题:
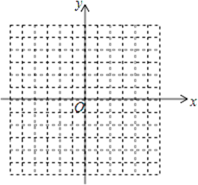
( 1 )请在如图坐标系中画出△ABC;
( 2 )画出△ABC关于y轴对称的△A'B'C',并写出△A'B'C'各顶点坐标。
21. 已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,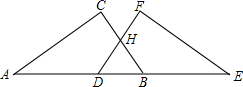 (1)、求证:△ABC≌△EDF;(2)、当∠CHD=120°,求∠HBD的度数.22. 为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元。设购进A种树苗x棵,购买两种树苗的总费用为w元。(1)、写出w(元)关于x(棵)的函数关系式;(2)、若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用。23. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y= x的图象交点为C(m,4).
(1)、求证:△ABC≌△EDF;(2)、当∠CHD=120°,求∠HBD的度数.22. 为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元。设购进A种树苗x棵,购买两种树苗的总费用为w元。(1)、写出w(元)关于x(棵)的函数关系式;(2)、若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用。23. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y= x的图象交点为C(m,4). (1)、求一次函数y=kx+b的解析式;(2)、求△BOC的面积;(3)、若点D在第二象限,△DAB为等腰直角三角形,则点D的坐标为.24. 问题背景
(1)、求一次函数y=kx+b的解析式;(2)、求△BOC的面积;(3)、若点D在第二象限,△DAB为等腰直角三角形,则点D的坐标为.24. 问题背景如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)
 (1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.(2)、△DEF是否为正三角形?请说明理由.(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
(1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.(2)、△DEF是否为正三角形?请说明理由.(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.