浙江省丽水市松阳县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,点(﹣2,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 以下是四位同学在钝角三角形ABC中画BC边上的高,其中画法正确的是( )A、
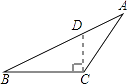 B、
B、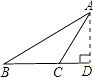 C、
C、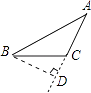 D、
D、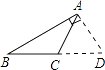 3. 已知 ,则下列不等式成立的是A、 B、 C、 D、4. 下列命题是真命题的是( )A、直角三角形中两个锐角互补 B、相等的角是对顶角 C、同旁内角互补,两直线平行 D、若 ,则5. 已知直角三角形的两条边长分别是3cm和4cm,则它的第三边长为( )A、4cm B、 cm C、5cm D、5cm或 cm6. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 不等式组 的解集是x>1,则m的取值范围是( )A、m≥1 B、m≤1 C、m≥0 D、m≤08. 一个装有进水管和出水管的容器,开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分钟的进水量和出水量是两个常数. 容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图,则6分钟时容器内的水量(单位:升)为( )
3. 已知 ,则下列不等式成立的是A、 B、 C、 D、4. 下列命题是真命题的是( )A、直角三角形中两个锐角互补 B、相等的角是对顶角 C、同旁内角互补,两直线平行 D、若 ,则5. 已知直角三角形的两条边长分别是3cm和4cm,则它的第三边长为( )A、4cm B、 cm C、5cm D、5cm或 cm6. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 不等式组 的解集是x>1,则m的取值范围是( )A、m≥1 B、m≤1 C、m≥0 D、m≤08. 一个装有进水管和出水管的容器,开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,每分钟的进水量和出水量是两个常数. 容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图,则6分钟时容器内的水量(单位:升)为( ) A、22 B、22.5 C、23 D、259. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A、22 B、22.5 C、23 D、259. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( ) A、 B、5 C、6 D、810. 如图,将点A0(-2,1)作如下变换:作A0关于x轴对称点,再往右平移1个单位得到点A1 , 作A1关于x轴对称点,再往右平移2个单位得到点A2 , …,作An-1关于x轴对称点,再往右平移n个单位得到点An(n为正整数),则点A64的坐标为( )
A、 B、5 C、6 D、810. 如图,将点A0(-2,1)作如下变换:作A0关于x轴对称点,再往右平移1个单位得到点A1 , 作A1关于x轴对称点,再往右平移2个单位得到点A2 , …,作An-1关于x轴对称点,再往右平移n个单位得到点An(n为正整数),则点A64的坐标为( ) A、(2078,-1) B、(2014 ,-1) C、(2078 ,1) D、(2014 ,1)
A、(2078,-1) B、(2014 ,-1) C、(2078 ,1) D、(2014 ,1)二、填空题
-
11. △ABC中,∠C=90°,∠A=54°,则∠B=°.12.
如图,点P在∠AOB的平分线上,若使△AOP≌△BOP,则需添加的一个条件是 (只写一个即可,不添加辅助线).
 13. 对于一次函数y=−2x+1,当−2<x<3时,函数值y的取值范围是.14. 等腰三角形的两边长分别为2和4,则其周长为 .
13. 对于一次函数y=−2x+1,当−2<x<3时,函数值y的取值范围是.14. 等腰三角形的两边长分别为2和4,则其周长为 .
15. 如图正方形ABCD分割成为七巧板迷宫,点E,F分别是CD,BC的中点,一只蚂蚁从D处沿图中虚线爬行到出口F处,若AB=2,则它爬行的最短路径长为. 16. 如图,在△ABC中,∠ACB=90°, AC=6cm, BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.(1)当t=.时,线段AP是∠CAB的平分线;(2)当t=时,△ACP是以AC为腰的等腰三角形.
16. 如图,在△ABC中,∠ACB=90°, AC=6cm, BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.(1)当t=.时,线段AP是∠CAB的平分线;(2)当t=时,△ACP是以AC为腰的等腰三角形.
三、解答题
-
17. 解不等式组 ,并把解集在数轴上表示出来.
 18. △ABC 在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.
18. △ABC 在平面直角坐标系中的位置如图所示,A,B,C三点在格点上. (1)、作出△ABC关于x 轴对称的△A1B1C1 , 并写出点C1的坐标;(2)、并求出△A1B1C1的面积.19. 已知△ABC中,AB=AC,CD⊥AB于D.
(1)、作出△ABC关于x 轴对称的△A1B1C1 , 并写出点C1的坐标;(2)、并求出△A1B1C1的面积.19. 已知△ABC中,AB=AC,CD⊥AB于D. (1)、若∠A=38º,求∠DCB的度数;(2)、若AB=5,CD=3,求△BCD的面积.20. 某学校开展美丽校园建设,计划购进A,B两种树苗共21棵,已知A种树苗每棵80元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)、求y与x的函数表达式,其中0≤x≤21;(2)、若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.21. 如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.
(1)、若∠A=38º,求∠DCB的度数;(2)、若AB=5,CD=3,求△BCD的面积.20. 某学校开展美丽校园建设,计划购进A,B两种树苗共21棵,已知A种树苗每棵80元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)、求y与x的函数表达式,其中0≤x≤21;(2)、若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.21. 如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上. (1)、求证:△AOC≌△BOD;(2)、若AD=1,BD=2,求CD的长.22. 某初级中学师生开展 “缅怀革命先烈,传承红色基因”为主题的研学活动.师生乘坐大巴先行出发. 通讯员15分钟后开小汽车出发,行驶过程发现某处风景优美,停下欣赏拍照15分钟,再以相同速度继续行驶,并提前6分钟到达目的地. 假设两车匀速行驶. 两车离出发点的距离s与 的函数关系如图,
(1)、求证:△AOC≌△BOD;(2)、若AD=1,BD=2,求CD的长.22. 某初级中学师生开展 “缅怀革命先烈,传承红色基因”为主题的研学活动.师生乘坐大巴先行出发. 通讯员15分钟后开小汽车出发,行驶过程发现某处风景优美,停下欣赏拍照15分钟,再以相同速度继续行驶,并提前6分钟到达目的地. 假设两车匀速行驶. 两车离出发点的距离s与 的函数关系如图,
试根据图象解决下列问题:
(1)、大巴车的速度千米/小时,小汽车的速度千米/小时;(2)、求大巴车出发后几个小时被小汽车第二次追上?23. 问题背景如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)
 (1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.(2)、△DEF是否为正三角形?请说明理由.(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.24. 如图,在长方形ABCO中,点O为坐标原点,点B的坐标为(8,6),点A,C在坐标轴上,直线y=2x+b经过点A且交x轴于点F.
(1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.(2)、△DEF是否为正三角形?请说明理由.(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.24. 如图,在长方形ABCO中,点O为坐标原点,点B的坐标为(8,6),点A,C在坐标轴上,直线y=2x+b经过点A且交x轴于点F. (1)、求b的值和△AFO的面积;(2)、将直线y=2x+b向右平移6单位后交AB于点D,交y轴于点E;
(1)、求b的值和△AFO的面积;(2)、将直线y=2x+b向右平移6单位后交AB于点D,交y轴于点E;①求点D,E的坐标;
②动点P在BC边上,点Q是坐标平面内第一象限内的点,且在平移后的直线上,若△APQ是等腰直角三角形,求点Q的坐标.