浙江省丽水市青田县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 下列坐标点在第四象限的是( )A、 B、 C、 D、2. 如图所示在 中, 边上的高线画法正确的是( )A、
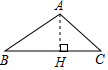 B、
B、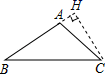 C、
C、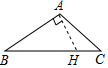 D、
D、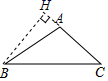 3.
3.已知两个不等式的解集在数轴上如右图表示,那么这个解集为( )
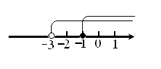 A、x≥-1 B、x>1 C、-3<x≤-1 D、x>-34. 如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )A、13 B、17 C、13或17 D、以上都不是5. 如图, ≌ ,下列结论正确的是( )
A、x≥-1 B、x>1 C、-3<x≤-1 D、x>-34. 如果一个等腰三角形的两条边长分别为3和7,那么这个等腰三角形的周长为( )A、13 B、17 C、13或17 D、以上都不是5. 如图, ≌ ,下列结论正确的是( ) A、 B、 C、 D、6. 直角三角形的两条边长分别是5和12,它的斜边长为( )A、13 B、 C、13或12 D、13或7. 若 成立,则下列不等式成立的是( )A、 B、 C、 D、8. 已知关于x的一次函数y=(2﹣m)x+2的图象如图所示,则实数m的取值范围为( )
A、 B、 C、 D、6. 直角三角形的两条边长分别是5和12,它的斜边长为( )A、13 B、 C、13或12 D、13或7. 若 成立,则下列不等式成立的是( )A、 B、 C、 D、8. 已知关于x的一次函数y=(2﹣m)x+2的图象如图所示,则实数m的取值范围为( )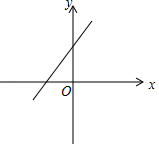 A、m>2 B、m<2 C、m>0 D、m<09. 如图,点A,B,C都在方格纸的“格点”上,请找出“格点”D,使点A,B,C,D组成一个轴对称图形,这样的点D共有( )个.
A、m>2 B、m<2 C、m>0 D、m<09. 如图,点A,B,C都在方格纸的“格点”上,请找出“格点”D,使点A,B,C,D组成一个轴对称图形,这样的点D共有( )个.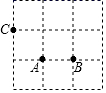 A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中有一个3×3的正方形网格,其右下角格点(小正方形的顶点)A的坐标为(﹣1,1),左上角格点B的坐标为(﹣4,4),若分布在过定点(﹣1,0)的直线y=﹣k(x+1)两侧的格点数相同,则k的取值可以是( )
A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中有一个3×3的正方形网格,其右下角格点(小正方形的顶点)A的坐标为(﹣1,1),左上角格点B的坐标为(﹣4,4),若分布在过定点(﹣1,0)的直线y=﹣k(x+1)两侧的格点数相同,则k的取值可以是( ) A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
11. 在平面直角坐标系中,点 关于 轴对称的点的坐标为.12. 用不等式表示x的3倍与5的和不大于10是;13. 如图, ,则 的度数为;
 14. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=75°,则∠BDF的度数为.
14. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=75°,则∠BDF的度数为. 15. 如图,在锐角三角形ABC中,AB=10,S△ABC=30,∠ABC的平分线BD交AC于点D,点M、N分别是BD和BC上的动点,则CM+MN的最小值是.
15. 如图,在锐角三角形ABC中,AB=10,S△ABC=30,∠ABC的平分线BD交AC于点D,点M、N分别是BD和BC上的动点,则CM+MN的最小值是. 16. 在平面直角坐标系中, 的顶点B在原点O,直角边BC,在x轴的正半轴上, ,点A的坐标为 ,点D是BC上一个动点(不与B,C重合),过点D作 交AB边于点E,将 沿直线DE翻折,点B落在x轴上的F处.
16. 在平面直角坐标系中, 的顶点B在原点O,直角边BC,在x轴的正半轴上, ,点A的坐标为 ,点D是BC上一个动点(不与B,C重合),过点D作 交AB边于点E,将 沿直线DE翻折,点B落在x轴上的F处.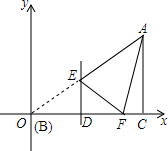 (1)、 的度数是;(2)、当 为直角三角形时,点E的坐标是.17. 解不等式组18. 如图
(1)、 的度数是;(2)、当 为直角三角形时,点E的坐标是.17. 解不等式组18. 如图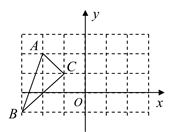 (1)、如图,已知 的顶点在正方形方格点上每个小正方形的边长为1.写出 各顶点的坐标(2)、画出 关于y轴的对称图形19. 已知:如图,在 中,点D在边AC上,BC与DE交于点P,AB=DB,
(1)、如图,已知 的顶点在正方形方格点上每个小正方形的边长为1.写出 各顶点的坐标(2)、画出 关于y轴的对称图形19. 已知:如图,在 中,点D在边AC上,BC与DE交于点P,AB=DB, (1)、求证:(2)、若AD=2,DE=5,BE=4,求 的周长之和.20. 已知:y-2与x成正比例,且x=2时,y=4.(1)、求y与x之间的函数关系式;(2)、若点M(m,3)在这个函数的图象上,求点M的坐标。21. 如图,在 中, 于D
(1)、求证:(2)、若AD=2,DE=5,BE=4,求 的周长之和.20. 已知:y-2与x成正比例,且x=2时,y=4.(1)、求y与x之间的函数关系式;(2)、若点M(m,3)在这个函数的图象上,求点M的坐标。21. 如图,在 中, 于D (1)、若 ,求 的度数(2)、若点E在AB上,EF//AC交AD的延长线于点F
(1)、若 ,求 的度数(2)、若点E在AB上,EF//AC交AD的延长线于点F求证:AE=FE
22. 我县电力部门实行两种电费计价方法,方法一是使用峰谷电:每天8:00至22:00用电每千瓦时收费0.56元(峰电价);22:00到次日8:00,每千瓦时收费0.28元(谷电价),方法二是不使用峰谷电:每千瓦时均收费0.53元(1)、如果小林家使用峰谷电后,上月付费95.2元,比不使用峰谷电少付费10.8元,则上月使用峰电和谷电各是多少千瓦时?(2)、如果小林家上月总用电量140千瓦时,那么当峰电用量为多少时,使用峰谷电比较合算.23. 如图在 中, ,将三角板中30度角的顶点D放在AB边上移动,使这个30度角的两边分别与 的边AC,BC相交于点E,F,且使DE,始终与AB垂直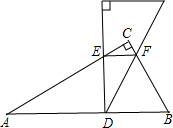 (1)、求证: 是等边三角形(2)、若移动点D,使EF//AB时,求AD的长24. 如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B,过点B的直线x轴于点C,且AB=BC.
(1)、求证: 是等边三角形(2)、若移动点D,使EF//AB时,求AD的长24. 如图,在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B,过点B的直线x轴于点C,且AB=BC. (1)、求直线BC的表达式(2)、点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,PQ交x轴于点P,设点Q的横坐标为m,求 的面积(用含m的代数式表示)(3)、在(2)的条件下,点M在y轴的负半轴上,且MP=MQ,若 求点P的坐标.
(1)、求直线BC的表达式(2)、点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,PQ交x轴于点P,设点Q的横坐标为m,求 的面积(用含m的代数式表示)(3)、在(2)的条件下,点M在y轴的负半轴上,且MP=MQ,若 求点P的坐标.