浙江省嘉兴市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 下列图标是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各点属于第二象限的是( )A、 B、 C、 D、3. 如果一个三角形的两边长分别为3和4,则第三边的长可能是( )A、6 B、8 C、10 D、124. 若 是直线 上一点,则 的值是( )A、2 B、-2 C、1 D、-15. 中, ,则 的度数为( )A、50° B、60° C、70° D、80°6. 下列说法不一定成立的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 已知 和 在一次函数 为常数)的图象上,且 ,则 的值可能是( )A、-2 B、-1 C、0 D、28. 如图, 中, 是 的中点, ,垂足为 .若 ,则 的长度是( )
2. 下列各点属于第二象限的是( )A、 B、 C、 D、3. 如果一个三角形的两边长分别为3和4,则第三边的长可能是( )A、6 B、8 C、10 D、124. 若 是直线 上一点,则 的值是( )A、2 B、-2 C、1 D、-15. 中, ,则 的度数为( )A、50° B、60° C、70° D、80°6. 下列说法不一定成立的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则7. 已知 和 在一次函数 为常数)的图象上,且 ,则 的值可能是( )A、-2 B、-1 C、0 D、28. 如图, 中, 是 的中点, ,垂足为 .若 ,则 的长度是( ) A、4 B、6 C、8 D、109. 如图,将一块含 45° 角的直角三角板 放置在直角坐标系中,直角顶点 ,点 在第一象限,则点 的坐标为( )
A、4 B、6 C、8 D、109. 如图,将一块含 45° 角的直角三角板 放置在直角坐标系中,直角顶点 ,点 在第一象限,则点 的坐标为( ) A、 B、 C、 D、10. 如图,四边形ABCD中,∠A、∠B 、∠C、 ∠D 的角平分线恰相交于一点P,记作△APD、△APB、△BPC、△DPC的面积分别为 、 、 、 则下列关系式正确的是( )
A、 B、 C、 D、10. 如图,四边形ABCD中,∠A、∠B 、∠C、 ∠D 的角平分线恰相交于一点P,记作△APD、△APB、△BPC、△DPC的面积分别为 、 、 、 则下列关系式正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. “两直线平行,内错角相等”的逆命题是 .12. 根据数量“ 的 倍与 的和大于 ”,列不等式为 .13. 如图,在 中, .则 的度数是 .
 14. 如图,已知 ,要使 ,需添加的一个条件是 .
14. 如图,已知 ,要使 ,需添加的一个条件是 . 15. 小红网购了一本数学拓展教材《好玩的数学》.两位小伙伴想知道书的价格,小红告诉他们这本书的价格是整数并让他们猜,小曹说:“至少29元”,小强说:“至多21元,小红说:“你们两个人都猜错了。从上述三人的对话中这本节的价格为元.16. 如图,在 中, 的平分线交 于点 ,若 ,则 的面积为 .
15. 小红网购了一本数学拓展教材《好玩的数学》.两位小伙伴想知道书的价格,小红告诉他们这本书的价格是整数并让他们猜,小曹说:“至少29元”,小强说:“至多21元,小红说:“你们两个人都猜错了。从上述三人的对话中这本节的价格为元.16. 如图,在 中, 的平分线交 于点 ,若 ,则 的面积为 .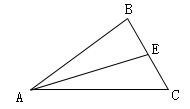 17. 如图,已如长方形纸片 是 边上一点, 为 中点,沿 折叠使得顶点 落在 边上的点 处,则 的度数是 .
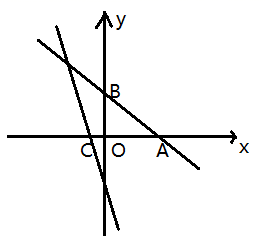
17. 如图,已如长方形纸片 是 边上一点, 为 中点,沿 折叠使得顶点 落在 边上的点 处,则 的度数是 .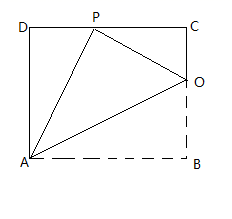 18. 如图,直线 交 轴于点 ,交直线 于点 ,则根据图象可知, 不等式的解为.
18. 如图,直线 交 轴于点 ,交直线 于点 ,则根据图象可知, 不等式的解为. 19. 平面直角坐标系中,点 ,当时, 的值最小.
19. 平面直角坐标系中,点 ,当时, 的值最小.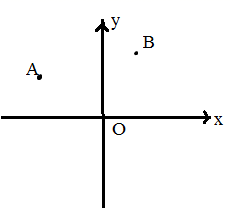 20. 如图, 是边长为 的等边三角形 内一点, 分别垂直于 ,垂足为 .若 ,则 .
20. 如图, 是边长为 的等边三角形 内一点, 分别垂直于 ,垂足为 .若 ,则 .
三、解答题
-
21. 已知一次函数 ,当 .(1)、求 的值(2)、当 ,求 的值22. 解不等式 ,把解表示在数轴上23. 已知:如图,点 在同一条直线上, .
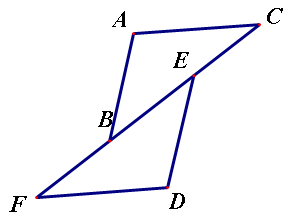 (1)、求证:(2)、若 ,求 的度数24. 如图是小明放学骑车回家行驶的路程 (千米)与行驶时间 分钟)的函数图象,已知前10分钟的速度是0.2千米分钟,行驶10分钟时车子发生故障,维修车子用了5分钟.然后又骑了5分钟到家,总共骑行了3.5千米,求最后5分钟小明的速度?
(1)、求证:(2)、若 ,求 的度数24. 如图是小明放学骑车回家行驶的路程 (千米)与行驶时间 分钟)的函数图象,已知前10分钟的速度是0.2千米分钟,行驶10分钟时车子发生故障,维修车子用了5分钟.然后又骑了5分钟到家,总共骑行了3.5千米,求最后5分钟小明的速度?