浙江省杭州市萧山区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 点 向左平移3个单位后所得点的坐标为( )A、 B、 C、 D、2. 直线 与 轴的交点坐标为( )A、 B、 C、 D、3. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、
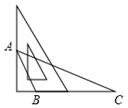 B、
B、 C、
C、 D、
D、 4. 用不等式表示:“ 的 与 的和为正数”,正确的是( )A、 B、 C、 D、5. 如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是( )
4. 用不等式表示:“ 的 与 的和为正数”,正确的是( )A、 B、 C、 D、5. 如图,在△ABC 中,AB=AC,∠B=50°,P 是边 AB 上的一个动点(不与顶点 A 重合),则∠BPC 的度数可能是( )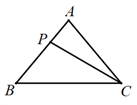 A、50° B、80° C、100° D、130°6. 已知 , 为一次函数 的图象上的两个不同的点,且 .若 , ,则 与 的大小关系是( )A、 B、 C、 D、 , 大小与点的位置有关7. 已知关于 的不等式组 有解,则 的取值不可能是( )A、0 B、1 C、2 D、-28. 如图,把 先沿着一条直线 进行轴对称变换,再沿着与这条直线平行的方向平移得到 ,则此两个三角形的对应点所具有的性质是( )
A、50° B、80° C、100° D、130°6. 已知 , 为一次函数 的图象上的两个不同的点,且 .若 , ,则 与 的大小关系是( )A、 B、 C、 D、 , 大小与点的位置有关7. 已知关于 的不等式组 有解,则 的取值不可能是( )A、0 B、1 C、2 D、-28. 如图,把 先沿着一条直线 进行轴对称变换,再沿着与这条直线平行的方向平移得到 ,则此两个三角形的对应点所具有的性质是( ) A、对应点连线与对称轴垂直 B、对应点连线被对称轴平分 C、对应点连线都相等 D、对应点连线互相平行9. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
A、对应点连线与对称轴垂直 B、对应点连线被对称轴平分 C、对应点连线都相等 D、对应点连线互相平行9. 一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:会员年卡类型
办卡费用(元)
每次游泳收费(元)
A 类
50
25
B 类
200
20
C 类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为( )
A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡10. 已知命题:①两边和第三边上的中线对应相等的两个三角形全等;②腰长和面积对应相等的两个等腰三角形全等,则下列判断正确的是( )A、①,②都是真命题 B、①是真命题,②是假命题 C、①是假命题,②是真命题 D、①,②都是假命题二、填空题
-
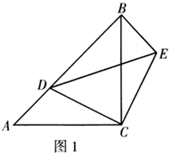
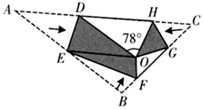
11. 满足 的最大整数是.12. 在平面直角坐标系 中,点 与点 关于(填写 或 )轴对称.13. 如图,将 沿 , , 翻折,三个顶点均落在点 处,且 与 重合于线段 ,若 ,则 的度数为.
 14. 已知直线 经过点 ,其中 ,则 的值为.15. 如图,在 中, , .已知 的中垂线 交 于点 ,交 于点 ,则 的值是.
14. 已知直线 经过点 ,其中 ,则 的值为.15. 如图,在 中, , .已知 的中垂线 交 于点 ,交 于点 ,则 的值是. 16. 沿河岸有 , , 三个港口,甲、乙两船同时分别从 , 港口出发,匀速驶向 港,最终到达 港.设甲、乙两船行驶 后,与 港的距离分别为 , , , 与 的函数关系如图所示.则:
16. 沿河岸有 , , 三个港口,甲、乙两船同时分别从 , 港口出发,匀速驶向 港,最终到达 港.设甲、乙两船行驶 后,与 港的距离分别为 , , , 与 的函数关系如图所示.则:
①从 港到 港全程为 ;
②如果两船相距小于 能够相互望见,那么在甲船到达 港前甲、乙两船可以相互望见时, 的取值范围是.
三、解答题
-
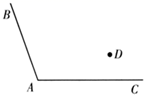
17. 解不等式组: .18. 如图, 和点 .在 内部,试求作一点 ,使得点 到 两边的距离相等,同时到点 , 的距离也相等.(不写作法,保留作图痕迹)
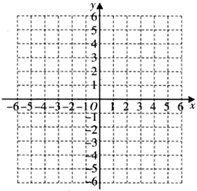
 19. 如图,有正方形网格(每个小正方形边长为1),按要求作图并解答:
19. 如图,有正方形网格(每个小正方形边长为1),按要求作图并解答:
( 1 )在网格中画出平面直角坐标系,使点 , ,并写出点 的坐标.
( 2 )平移 ,使点 平移后所得的点是 .
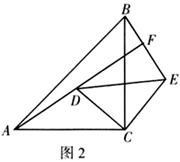
20. 已知 关于 的一次函数 .(1)、若此函数图象经过点 ,当 时,求 的取值范围.(2)、若此一次函数图象经过第一、二、四象限,求 的取值范围.21. 如图,在等边 中,点 , 分别是 , 上的点,将 沿 所在直线对折,点 落在 边上的点 处,且 .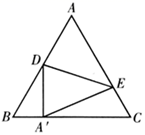 (1)、求 的度数.(2)、若 ,求线段 的值.
(1)、求 的度数.(2)、若 ,求线段 的值.