浙江省杭州市下城区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-11-02 类型:期末考试
一、选择题
-
1. 在 中,若 ,则 是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形2. 设AD是 的中线,则( )A、 B、 C、 D、3. 用不等式表示“y减去1不大于2”,正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,位于第二象限的点( )A、横坐标小于纵坐标 B、横坐标大于纵坐标 C、横坐标与纵坐标的和小于0 D、横坐标与纵坐标的积大于05. 若等腰三角形的底边长为10,则腰长可以是( )A、1 B、3 C、5 D、76. 设P1(x1,y1),P2(x2,y2)是一次函数y=-2x+b图象上的两点,则( )A、y1>y2 B、y1<y2 C、当x1<x2时,y1>y2 D、当x1<x2时,y1<y27. 将一副三角板按不同位置放置,其中 与 互补的是( )A、
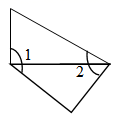 B、
B、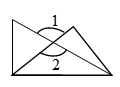 C、
C、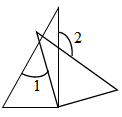 D、
D、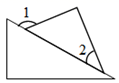 8. 设m,n是实数,a,b是正整数,若 ,则( )A、 B、 C、 D、9. 甲,乙两人分别从A,B两地出发相向而行, 分别表示甲,乙两人离B地的距离 与行走时间 之间的关系,设甲,乙行走的速度分别是 和 ,则( ).
8. 设m,n是实数,a,b是正整数,若 ,则( )A、 B、 C、 D、9. 甲,乙两人分别从A,B两地出发相向而行, 分别表示甲,乙两人离B地的距离 与行走时间 之间的关系,设甲,乙行走的速度分别是 和 ,则( ).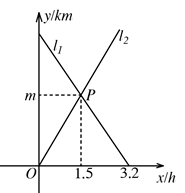 A、 B、 C、 D、10. 如图:在 中, , 于点D,点P在线段DB上,点M是边AC的中点,连结MP,作 ,点Q在边BC上.若 ,则( )
A、 B、 C、 D、10. 如图:在 中, , 于点D,点P在线段DB上,点M是边AC的中点,连结MP,作 ,点Q在边BC上.若 ,则( )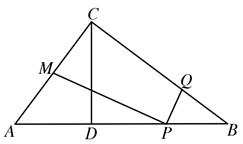 A、当 时,点P与点D重合 B、当 时, C、当 时, D、当 时,
A、当 时,点P与点D重合 B、当 时, C、当 时, D、当 时,二、填空题
-
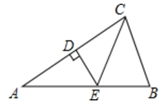
11. 命题“若 ,则 ”的条件是12. 在平面直角坐标系中,若点 在x轴上,则点P的坐标是.13. 如图,在 中,AC的垂直平分线分别与边AC,边AB交FDE,连结CE。若 , ,则 .
 14. 在平面直角坐标系中,点A(a,-3)向左平移3个单位得点A’,若点A和A’关于y轴对称,则a=.15. 德国数学家莱布尼兹证明了 ,由此可知: (填“>"或"<”)16. 点A(1,n1),点B(2,n2)在一次函数y1=k1x+b1图象上:点C(3,n3),点D(4,n4)在一次函数y2=k2x+b2图象上,y1 和y2图象交点坐标是(m,n).若n4<n1<n3<n2 , 则下列说法:①k1>0,k2<0;②k1<0,k2>0;③1<m<3;④2<m<4,正确的是(填序号).
14. 在平面直角坐标系中,点A(a,-3)向左平移3个单位得点A’,若点A和A’关于y轴对称,则a=.15. 德国数学家莱布尼兹证明了 ,由此可知: (填“>"或"<”)16. 点A(1,n1),点B(2,n2)在一次函数y1=k1x+b1图象上:点C(3,n3),点D(4,n4)在一次函数y2=k2x+b2图象上,y1 和y2图象交点坐标是(m,n).若n4<n1<n3<n2 , 则下列说法:①k1>0,k2<0;②k1<0,k2>0;③1<m<3;④2<m<4,正确的是(填序号).三、解答题
-
17. 解一元一次不等式组18. 如图, ,点E和点F在线段BC上, .
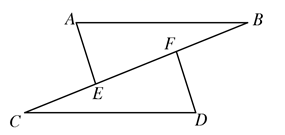 (1)、求证: .(2)、若 ,求BE的长19. 设一次函数 (k,b是常数, )的图象过 两点.(1)、求该一次函数的表达式.(2)、当 时,函数值y的取值范围是 ,分别求m和n的值.20. 在 中,点E,点F分别是边AC,AB上的点,且 ,连结BE,CF交于点D, .
(1)、求证: .(2)、若 ,求BE的长19. 设一次函数 (k,b是常数, )的图象过 两点.(1)、求该一次函数的表达式.(2)、当 时,函数值y的取值范围是 ,分别求m和n的值.20. 在 中,点E,点F分别是边AC,AB上的点,且 ,连结BE,CF交于点D, .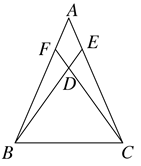 (1)、求证: 是等腰三角形.(2)、若 ,求 的度数.21. 已知 ,其中a,b,c是常数,且 .(1)、当 时,求a的范围.(2)、当 时,比较b和c的大小.(3)、若当 时, 成立,则 的值是多少?22. 一次函数y1=k(x-1)与一次函数y2=-k(x-3)的图象交于点P,其中k≠0.
(1)、求证: 是等腰三角形.(2)、若 ,求 的度数.21. 已知 ,其中a,b,c是常数,且 .(1)、当 时,求a的范围.(2)、当 时,比较b和c的大小.(3)、若当 时, 成立,则 的值是多少?22. 一次函数y1=k(x-1)与一次函数y2=-k(x-3)的图象交于点P,其中k≠0.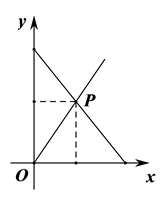 (1)、求点P的横坐标.(2)、点A(a,y)和点B(b,y)分别在y1和y2的图象上,若a=5,求b的值.(3)、点C(x,m)和点D(x,n)分别在y1和y2的图象上,若m-n>k,当k>0时,求x的取值范围.23. 在 中, ,CD是AB边上的高,若 .
(1)、求点P的横坐标.(2)、点A(a,y)和点B(b,y)分别在y1和y2的图象上,若a=5,求b的值.(3)、点C(x,m)和点D(x,n)分别在y1和y2的图象上,若m-n>k,当k>0时,求x的取值范围.23. 在 中, ,CD是AB边上的高,若 .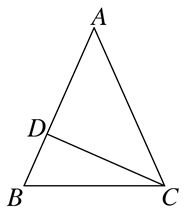 (1)、求CD的长.(2)、动点P在边AB上从点A出发向点B运动,速度为1个单位/秒;动点Q在边AC上从点A出发向点C运动,速度为v个单位秒 ,设运动的时间为 ,当点Q到点C时,两个点都停止运动.
(1)、求CD的长.(2)、动点P在边AB上从点A出发向点B运动,速度为1个单位/秒;动点Q在边AC上从点A出发向点C运动,速度为v个单位秒 ,设运动的时间为 ,当点Q到点C时,两个点都停止运动.①若当 时, ,求t的值.
②若在运动过程中存在某一时刻,使 成立,求v关于t的函数表达式,并写出自变量t的取值范围.