黑龙江省哈尔滨市香坊区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-11-02 类型:期末考试
一、单选题
-
1. 下列方程是一元一次方程的是( )A、2x+1=0 B、3x+2y=5 C、xy+2=3 D、x2=02. 下列图案中,可以利用平移来设计的图案是( )A、
 B、
B、 C、
C、 D、
D、 3. 在实数 , ,3.1415, 中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个4. 下列图形中,∠1和∠2不是同位角的是( )
3. 在实数 , ,3.1415, 中,无理数的个数是( )A、1个 B、2个 C、3个 D、4个4. 下列图形中,∠1和∠2不是同位角的是( )
A、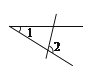 B、
B、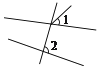 C、
C、 D、
D、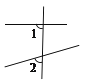 5. 运用等式性质进行的变形,正确的是( )A、如果a=b,那么a+2=b+3 B、如果a=b,那么a-2=b-3 C、如果 ,那么a=b D、如果a2=3a,那么a=36. 丽宏幼儿园王阿姨给小朋友分苹果,如果每人分3个.则剩余1个;如果每人分4个,则还缺2个.问有多少个苹果?设幼儿园有x个小朋友,则可列方程为( )A、3x﹣1=4x+2 B、3x+1=4x﹣2 C、 D、7. 一个长方形在平面直角坐标系中,三个顶点的坐标分别是(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标是( )A、(2,2) B、(3,3) C、(3,2) D、(2,3)8. 某商场在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是( )A、盈利8元 B、亏损8元 C、不盈不亏 D、亏损15元9. 下列命题为假命题的是( )A、垂线段最短 B、两条直线相交,若邻补角相等,则这两条直线互相垂直 C、相等的角是对顶角 D、经过直线外一点,有且只有一条直线与这条直线平行10. 将一直角三角尺与两边平行的纸条按如图所示放置,下列结论:
5. 运用等式性质进行的变形,正确的是( )A、如果a=b,那么a+2=b+3 B、如果a=b,那么a-2=b-3 C、如果 ,那么a=b D、如果a2=3a,那么a=36. 丽宏幼儿园王阿姨给小朋友分苹果,如果每人分3个.则剩余1个;如果每人分4个,则还缺2个.问有多少个苹果?设幼儿园有x个小朋友,则可列方程为( )A、3x﹣1=4x+2 B、3x+1=4x﹣2 C、 D、7. 一个长方形在平面直角坐标系中,三个顶点的坐标分别是(﹣1,﹣1)、(﹣1,2)、(3,﹣1),则第四个顶点的坐标是( )A、(2,2) B、(3,3) C、(3,2) D、(2,3)8. 某商场在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是( )A、盈利8元 B、亏损8元 C、不盈不亏 D、亏损15元9. 下列命题为假命题的是( )A、垂线段最短 B、两条直线相交,若邻补角相等,则这两条直线互相垂直 C、相等的角是对顶角 D、经过直线外一点,有且只有一条直线与这条直线平行10. 将一直角三角尺与两边平行的纸条按如图所示放置,下列结论:
①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°.正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 3的相反数是;﹣1.5的倒数是 .12. 如果 x=2 是方程的ax-3=5 解,那么 a= .13. 比较大小: 4 (填“>”、“<”或“=”号).14. 将“对顶角相等”改写为“如果...那么...”的形式,可写为.15. 若点P(m﹣2,2m+1)在x轴上,则m的值是 .16. 一件服装的进价是200元,按标价的八折销售,仍可获利10%,该服装的标价是 .17. 在同一平面内,直线AB与直线CD相交于点O,∠BOC:∠BOD=4:5,射线OE⊥CD,则∠BOE的度数为.18. 有一列数,按一定规律排列成1,﹣3,9,﹣27,81,﹣243,…,其中某三个相邻数的和是﹣1701,这三个相邻数中的第一个数为 .19. 如图,在一块长为20m,为10m的长方形草地上,修建两条宽为2m的长方形小路,则这块草地的绿地面积(图中空白部分)为m2.
 20. 如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF=度.
20. 如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连接NE、NM,过点N作NG平分∠ENM,交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF=度.
三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 解方程:(1)、2x+5=3(x﹣1);(2)、 .23. 在如图所示的方格纸中,每个小正方形的边长都是1个单位长度,每个小正方形的顶点叫格点,三角形ABC的三个頂点都在格点上.
 (1)、画出三角形ABC向上平移4个单位后的三角形A1B1C1(点A,B,C的对应点为点A1 , B1 , C1);(2)、画出三角形A1B1C1向左平移5个单位后的三角形A2B2C2(点A1 , B1 , C1的对应点为点A2 , B2 , C2);(3)、分别连接AA1 , A1A2 , AA2 , 并直接写出三角形AA1A2的面积为平方单位.24. 已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
(1)、画出三角形ABC向上平移4个单位后的三角形A1B1C1(点A,B,C的对应点为点A1 , B1 , C1);(2)、画出三角形A1B1C1向左平移5个单位后的三角形A2B2C2(点A1 , B1 , C1的对应点为点A2 , B2 , C2);(3)、分别连接AA1 , A1A2 , AA2 , 并直接写出三角形AA1A2的面积为平方单位.24. 已知:直线AB与直线CD交于点O,过点O作OE⊥AB. (1)、如图1,∠BOC=2∠AOC,求∠COE的度数;(2)、如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.25. 某中学到商店购买足球和排球,购买足球40个,排球30个共花费4000元,已知购买一个足球比购买一个排球多花30元.(1)、求购买一个足球和一个排球各需多少元?(2)、学校决定第二次购买足球和排球共50个,正好赶上商场对商品价格进行调整,一个足球售价比第一次购买时提高了10%,一个排球按第一次购买时售价的九折出售,如果学校第二次购买足球和排球的总费用是第一次购买总费用的86%,求学校第二次购买排球多少个?26. 已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°.
(1)、如图1,∠BOC=2∠AOC,求∠COE的度数;(2)、如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.25. 某中学到商店购买足球和排球,购买足球40个,排球30个共花费4000元,已知购买一个足球比购买一个排球多花30元.(1)、求购买一个足球和一个排球各需多少元?(2)、学校决定第二次购买足球和排球共50个,正好赶上商场对商品价格进行调整,一个足球售价比第一次购买时提高了10%,一个排球按第一次购买时售价的九折出售,如果学校第二次购买足球和排球的总费用是第一次购买总费用的86%,求学校第二次购买排球多少个?26. 已知:直线AB与直线PQ交于点E,直线CD与直线PQ交于点F,∠PEB+∠QFD=180°. (1)、如图1,求证:AB∥CD;(2)、如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;(3)、如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.27. 已知:在平面直角坐标系中,点A的坐标为(m,0),点B的坐标为(0,n),其中m= , =0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.
(1)、如图1,求证:AB∥CD;(2)、如图2,点G为直线PQ上一点,过点G作射线GH∥AB,在∠EFD内过点F作射线FM,∠FGH内过点G作射线GN,∠MFD=∠NGH,求证:FM∥GN;(3)、如图3,在(2)的条件下,点R为射线FM上一点,点S为射线GN上一点,分别连接RG、RS、RE,射线RT平分∠ERS,∠SGR=∠SRG,TK∥RG,若∠KTR+∠ERF=108°,∠ERT=2∠TRF,∠BER=40°,求∠NGH的度数.27. 已知:在平面直角坐标系中,点A的坐标为(m,0),点B的坐标为(0,n),其中m= , =0,将三角形BOA沿x轴的正方向向右平移10个单位长度得到三角形CDE,连接BC.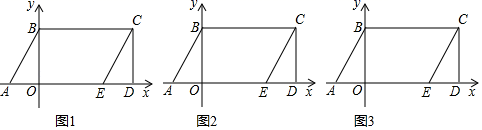 (1)、如图1,分别求点C、点E的坐标;(2)、点P自点C出发,以每秒1个单位长度沿线段CB运动,同时点Q自点O出发,以每秒2个单位长度沿线段OE运动,连接AP、BQ,点Q运动至点E时,点P同时停止运动.设运动时间t(秒),三角形ABQ的面积与三角形APB的面积的和为s(平方单位),求s与t的关系式,并直接写出t的取值范围;(3)、在(2)的条件下,BP:QE=8:3,此时将线段PQ向左平移2个单位长度得到线段P'Q'(点P'与点P对应),线段P′Q'再向下平移2个单位长度得到线段MN(点M与点P'对应),线段MN交x轴于点G,点H在线段OA上,OH= OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.
(1)、如图1,分别求点C、点E的坐标;(2)、点P自点C出发,以每秒1个单位长度沿线段CB运动,同时点Q自点O出发,以每秒2个单位长度沿线段OE运动,连接AP、BQ,点Q运动至点E时,点P同时停止运动.设运动时间t(秒),三角形ABQ的面积与三角形APB的面积的和为s(平方单位),求s与t的关系式,并直接写出t的取值范围;(3)、在(2)的条件下,BP:QE=8:3,此时将线段PQ向左平移2个单位长度得到线段P'Q'(点P'与点P对应),线段P′Q'再向下平移2个单位长度得到线段MN(点M与点P'对应),线段MN交x轴于点G,点H在线段OA上,OH= OG,过点H作HR⊥OA,交AB于点R,求点R的坐标.