初中数学苏科版七年级上册4.3用一元一次方程解决问题 同步练习
试卷更新日期：2020-11-02 类型：同步测试
一、单选题
-
1. 有一些纸箱和若干梨．若每个纸箱装25千克梨，则余40千克无处装；若每个纸箱装30千克梨，则余20个空箱．这些纸箱有（ ）A、40个 B、60个 C、128个 D、130个2. 某汽车队运送一批救灾物资，若每辆车装4吨，还剩8吨未装；若每辆车装4.5吨，恰好装完.设这个车队有 辆车，则（ ）A、 B、 C、 D、3. 防范新冠病毒感染要养成戴口罩、勤洗手、多通风、常消毒等卫生习惯，其中对物体表面进行消毒可以采用浓度为75％的酒精.现有一瓶浓度为95％的酒精500mL，需将其加入适量的水，使浓度稀释为75％.设加水量为xml，可列方程为（ ）A、75％x＝95％×500 B、95％x＝75％×500 C、75％（500＋x）＝95％×500 D、95％（500＋x）＝75％×5004. 为了配合 “我读书，我快乐”读书节活动，某书店推出一种优惠卡，每张卡售价20元，凭卡购书可享受8折优惠，小慧同学到该书店购书，她先买优惠卡再凭卡付款，结果节省了10元，若此次小慧同学不买卡直接购书，则她需付款（ ）A、140元 B、150元 C、160元 D、200元5. 某班30位同学，在绿色护植活动中共种树72棵。已知女生每人种2棵，男生每人种3棵，设女生有x人，则可列方程（ ）A、2x+3(30-x)=72 B、3x+2(30-x)=72 C、2x+3(72-x)=30 D、3x+2(72-x)=306. 对于任意两个有理数a、b，规定a⊗b=3a﹣b，若（2x+3）⊗（3x﹣1）=4，则x的值为（ ）A、1 B、﹣1 C、2 D、﹣27. 天平呈平衡状态，其中左侧秤盘中有一袋玻璃球，右侧秤盘中也有一袋玻璃球，还有2个各20克的砝码．现将左侧袋中一颗玻璃球移至右侧秤盘，并拿走右侧秤盘的1个砝码后，天平仍呈平衡状态，如图2，则被移动的玻璃球的质量为（ ）
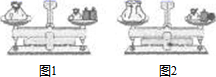A、10克 B、15克 C、20克 D、25克8. 已知今年甲的年龄比乙的年龄多12岁，4年后甲的年龄恰好是乙的年龄的2倍，则甲今年的年龄是（ ）A、20岁 B、16岁 C、15岁 D、12岁9. 兄弟四人共有450元钱，如果老大增加20元钱，老二减少20元钱，老三增加到原来的2倍，老四减少到原来的 ，这时候四人的钱同样多。针对他们原来的钱的数目，下列说法错误的是（ ）A、老四的钱是老三的4倍 B、老大与老二的钱总和等于老四的钱 C、老二的钱是老三的钱的2倍还多10元 D、老四的钱是老大的钱的3倍少40元10. 如图是某月的日历表，在此日历表上可以用一个矩形圈出3×3个位置的9个数（如6，7，8，13，14，15，20，21，22）．若用这样的矩形圈圈这张日历表的9个数，则圈出的9个数的和可能为下列数中的（ ）
A、81 B、100 C、108 D、216二、填空题
-
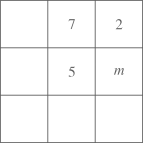
11. 六(7)班某天的出勤率是90%，那么缺勤人数与出勤人数的比是 ， 如果那天到校36人，那么六(7)班全班有人。12. 在一次考试中，甲、乙两同学的考试分数之比是5：4，如果甲少得22.5分，乙多得22.5分，那么甲、乙的得分之比就是5：7，甲原来得了分。13. 幻方是相当古老的数学问题，我国古代的《洛书》中记载了最早的幻方---九宫图.将数字1~9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则m的值为.
14. 足球比赛的计分规则为：胜一场积3分，平一场积1分，负1场积0分． 初三．（1）班在校足球联赛中踢了17场，其中负4场，共积31分，那么这支足球队胜了场．15. 若代数式 与 的值互为相反数，则 ．16. 如图1是边长为18cm的正方形纸板，剪掉阴影部分后将其折叠成如图2所示的长方体盒子．已知该长方体的宽是高的2倍，则它的体积是 ．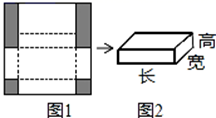
17. 如图，天平两边盘中标有相同字母的物体的质量相同，若A物体的质量为20克，当天平处于平衡状态时，B物体的质量为克.
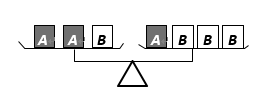18. 明代珠算大师程大位著有《珠算统宗》一书，有下面的一道题：“隔墙听得客分银，不知人数不知银，七两分之多四两，九两分之少半斤(1斤等于16两)”.据此可知，客有人，银有两.三、解答题
-
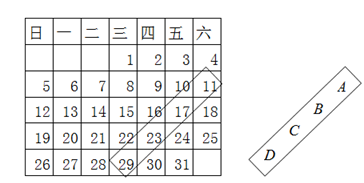
19. 课外活动中一些学生分组参加活动，原来每组6人，后来重新编组，每组8人，这样就比原来减少2组，问这些学生共有多少人？20. 力“皖”狂澜，新冠肺炎期间，安徽共出动八批，共计1362位医护人员驰援武汉，他们是新时代最可爱的人.3月19日，第二批和第八批医护人员共130人乘坐飞机返回合肥，其中第二批人数是第八批人数的3倍还多10人，第八批安徽共出动了多少名医护人员？21. 长春某旅行社组织甲、乙两个旅行团分别到西安、北京旅游，已知这两个旅游团共有55人，甲旅游团的人数比乙旅游团的人数的2倍少5人，问甲、乙两个旅游团各有多少人？22. 张翔从学校出发骑自行车去县城，中途因道路施工步行一段距离，1.5h后到达县城．他骑车的平均速度是15km/h，步行的平均速度是5km/h，路程长20km，他骑车与步行各用多少时间？23. 如图是2020年1月的日历，小明用矩形按图示方向从中任意框出4个日期，若这四个 日期的和为68，则C处上的日期是1月几日?
24. 一个两位数，把它的个位数字与十位数字交换位置得到新两位数，原两位数的个位数字比原两位数的十位数字大2，且新两位数与原两位数的和为154，求原两位数是多少？25. 甲对乙说：“我像你现在这么大时，你的年龄是我现在年龄的一半；你像我现在这么大时，我们俩的年龄和是63岁．”问甲、乙两人今年各是多少岁?26. 列方程解应用题．明代商人程大位在《算法统宗》里记载了一道趣题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完．试问大、小和尚各多少人？
27. 《孙子算经）是我国传统数学的重要著作之一，其中记载的“荡杯问题”非常有趣．原题是今有妇人河上荡杯，津吏问曰：“杯何以多？”妇人曰：“有客．”津吏曰：“客几何？”妇人曰：“两人共饭，三人共羹，四人共肉，凡用杯六十五．不知客几何？”大意：一个妇女在河边洗碗，河官问：“洗多少碗？有多少客？”妇女答：“洗 只碗，客人二人．共用一只饭碗，三人共用一只汤碗，四人共用一只肉碗．问：有多少客人用餐？”请解答上述问题．