黑龙江省哈尔滨市道里区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-11-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，属于无理数的是（）

A、 $\frac{22}{7}$ B、1.414 C、 $\sqrt{2}$ D、 $\sqrt{4}$

查看试题解析
2. 如图所示，A、B、C、D四幅图案中，能通过平移图案（1）得到的是（）

A、 B、 C、 D、

查看试题解析
3. 在平面直角坐标系中，点 $A (- 5, 4)$ 所在的象限为（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 根据等式的性质，下列各式变形正确的是（）

A、若 $3 x = 5$ ，则 $\frac{3 x}{a} = \frac{5}{a}$ B、若 $x = y$ ，则 $x - 6 = 6 - y$ C、如果 $x = y$ ，那么 $- 8 x = - 8 y$ D、 $2 x = 6$ ，那么 $x = \frac{1}{3}$

查看试题解析
5. 点 $P (a - 2 ， a + 1)$ 在 $x$ 轴上，则a的值为（）

A、2 B、0 C、1 D、-1

查看试题解析
6. 如图，已知两直线 $l_{1}$ 与 $l_{2}$ 被第三条直线 $l_{3}$ 所截，下列等式一定成立的是（）

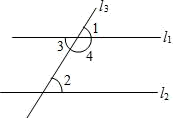A、 $∠ 1 = ∠ 2$ B、 $∠ 2 = ∠ 3$ C、 $∠ 2 + ∠ 4$ =180° D、 $∠ 1 + ∠ 4$ =180°

查看试题解析
7. 面积为4的正方形的边长是（）

A、4的平方根 B、4的算术平方根 C、4开平方的结果 D、4的立方根

查看试题解析
8. 一项工程甲单独做要40天完成，乙单独做需要60天完成，甲先单独做4天，然后甲乙两人合作 $x$ 天完成这项工程，则可以列的方程是（）

A、 $\frac{4}{40} + \frac{x}{40 + 60} = 1$ B、 $\frac{4}{40} + \frac{x}{40 \times 60} = 1$ C、 $\frac{4}{40} + \frac{x}{40} + \frac{x}{60} = 1$ D、 $\frac{4}{40} + \frac{x}{60} = 1$

查看试题解析
9. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt[3]{- 5} = \sqrt[3]{5}$ C、 $\sqrt{36} = \pm 6$ D、 $- \sqrt{0.36} =-0 .6$

查看试题解析
10. 如图，点 $E$ 在 $B A$ 的延长线上，能证明 $B E // C D$ 是（）

A、 $∠ E A D = ∠ B$ B、 $∠ B A D = ∠ A C D$ C、 $∠ E A D = ∠ A C D$ D、 $∠ E A C + ∠ A C D = 180 °$

查看试题解析

二、填空题

11. 实数 $- \sqrt{2}$ 的相反数是.

查看试题解析
12. 若 $4$ 排 $3$ 列用有序数对 $(4, 3)$ 表示，那么表示 $2$ 排 $5$ 列的有序数对为．

查看试题解析
13. 如果 $∠ 1 = ∠ 2$ ， $∠ 2 = ∠ 3$ ，那么 $∠ 1 = ∠ 3$ ；该命题的结论是．

查看试题解析
14. 比 $a$ 的2倍大5的数等于 $a$ 的8倍，列等式表示为．

查看试题解析
15. 若 $(m - 2) x^{m^{2} - 3} = 5$ 是一元一次方程，则m的值是.

查看试题解析
16. 如图，CD⊥AB，点D为垂足，DE平分∠CDB，则∠ADE是度.

查看试题解析
17. 点 $O (a + 8 ， b - 2)$ 为坐标原点，则 $a^{b}$ 的立方根是．

查看试题解析
18. 几个人共同种一批树苗，如果每人种15棵，则剩下4棵树苗未种；如果每人种16棵树苗，则缺4棵树苗，则这批树苗共有棵．

查看试题解析
19. 点 $C$ 在 $∠ A O B$ 的边 $O A$ 上，过点 $C$ 作 $C D ⊥ O B$ ，过点 $C$ 作 $O A$ 的垂线交射线 $O B$ 于点 $E$ ，若 $∠ A O B = 66 °$ ，则 $∠ D C E$ 是度．

查看试题解析
20. 甲船从 $A$ 码头出发顺流驶向 $B$ 码头，同时乙船从 $B$ 码头出发逆流驶向 $A$ 码头，甲，乙两船到达 $B$ ， $A$ 两码头后立即返回，乙船返回后行驶20千米与返回的甲船相遇，甲，乙两船在静水中的平均速度不变， $A$ ， $B$ 两码头间的水流速度为4千米/时，甲船逆流而行的速度与乙船顺流而行的速度相等，甲船顺流而行速度是乙船逆流而行速度的2倍，则 $A$ ， $B$ 两码头间的路程为千米．

查看试题解析

三、解答题

21.

(1)、 $\sqrt{4} - \sqrt[3]{125} + \sqrt{{(- 3)}^{2}} - \sqrt[3]{\frac{1}{8}}$ ．

(2)、 $\sqrt{3} (\sqrt{3} - 2) + | 3 - 2 \sqrt{3} | - | \sqrt[3]{- 27} |$ ．

查看试题解析
22. 三角形 $A B C$ 在平面直角坐标系的位置如图.将三角形 $A B C$ 向右平移4个单位长度得到三角形 $A_{1} B_{1} C_{1}$ ，点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ，分别为 $A$ ， $B$ ， $C$ 的对应点．

(1)、画出三角形 $A_{1} B_{1} C_{1}$ ；

(2)、直接写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

查看试题解析
23. 解方程

(1)、 $2 x + 3 = 5 x - 6$ ．

(2)、 ${(x - 2)}^{2} = 9$ ．

(3)、 $\frac{1}{6} (3 x - 6) = \frac{5}{2} x - 5$ ．

(4)、 $3 - \frac{5 x + 2}{7} = \frac{1 + 8 x}{3} - x$ ．

查看试题解析
24. 如图，三角形 $A B C$ 中， $D$ 是 $A B$ 上一点， $E$ 是 $A C$ 上一点， $∠ A + ∠ A E F = 180 °$ ， $∠ E F C = ∠ A D E$ ， $E G ⊥ B C$ ，垂足为 $G$ ．求 $∠ D E G$ 是多少度？

查看试题解析
25. 某商店第一次购进相同铅笔1000支，第二次又购进同种铅笔，购进数量是第一次的 $\frac{1}{2}$ ，这次每支铅笔的进价比第一次进价高0.2元，第二次购进铅笔比第一次少花300元．

(1)、求第一次每支铅笔的进价是多少元？

(2)、第一次购进铅笔在第一次进价的基础上加价50%出售；第二次购进的铅笔以每支1.5元的价格出售，出售一部分后又在每支1.5元的基础上打八折出售；两次购进的铅笔全部销售完毕后总获利为560元，问第二次购进的铅笔出售多少支后打八折出售？

查看试题解析
26. 点 $C$ ， $B$ 分别在直线 $M N$ ， $P Q$ 上，点 $A$ 在直线 $M N$ ， $P Q$ 之间， $M N / / P Q$ ．

(1)、如图1，求证： $∠ A = ∠ M C A + ∠ P B A$ ；

(2)、如图2，过点 $C$ 作 $C D // A B$ ，点 $E$ 在 $P Q$ 上， $∠ E C M = ∠ A C D$ ，求证： $∠ A = ∠ E C N$ ；

(3)、在（2）的条件下，如图3，过点 $B$ 作 $P Q$ 的垂线交 $C E$ 于点 $F$ ， $∠ A B F$ 的平分线交 $A C$ 于点 $G$ ，若 $∠ D C E = ∠ A C E$ ， $∠ C F B = ∠ \frac{3}{2} C G B$ ，求 $∠ A$ 的度数．

查看试题解析
27. 在平面直角坐标系中，点 $O$ 为坐标原点，正方形 $O A B C$ 与长方形 $D E F G$ 的位置如图所示，点 $A$ 在 $x$ 轴的正半轴上，点 $C$ 在 $y$ 轴的正半轴上，点 $B$ 的横坐标为 $a$ ，点 $D$ ， $E$ 在 $x$ 轴的负半轴上（点 $E$ 在点 $D$ 的右侧），点 $G$ 的坐标为 $（ b ， - b ）$ ， $D E = O A$ ，实数 $a$ ， $b$ 的值满足 $\sqrt{a - 4} + \sqrt{b + 6} = 0$ .

(1)、求点 $F$ 的坐标；

(2)、长方形 $D E F G$ 以每秒1个单位长度的速度向右平移 $t$ （ $t > 0$ ）秒得到矩形 $D' E' F' G'$ ，点 $D'$ ， $E'$ ， $F'$ ， $G'$ 分别为点 $D$ ， $E$ ， $F$ ， $G$ 平移后的对应点，设矩形 $D' E' F' G'$ 与正方形 $O A B C$ 重合部分的面积为 $S$ ，用含 $t$ 的式子表示 $S$ ，并直接写出相应的 $t$ 的范围；

(3)、在（2）的条件下，在长方形 $D E F G$ 出发运动的同时，点 $P$ 从点 $O$ 出发，沿正方形的边以每秒2个单位长度的速度顺时针方向运动（即 $O \to C \to B \to A \to O \to C$ ），连接 $P D'$ ， $P G'$ ，当三角形 $P D' G'$ 的面积为15时，求 $S > 0$ 时相应的 $t$ 值，并直接写出此时刻 $S$ 值及点 $P$ 的坐标．

查看试题解析