浙江省杭州市西湖区2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-11-02 类型：期末考试

进入出卷网下载

一、选择题

1. 点 $A(-1，3)$ 向右平移3个单位，再向下平移3个单位，所得点的坐标为（）

A、 $(2，0)$ B、 $(2，3)$ C、 $(-4，6)$ D、 $(-4，0)$

查看试题解析
2. 若 $x - 3 < 0$ ，则（）

A、 $x - 2 > 0$ B、 $2 x > - 1$ C、 $2 x < 3$ D、 $18 - 3 x > 0$

查看试题解析
3. 有以下命题：
①同旁内角补，两直线平行；②若 $| a | = | b |$ ，则 $a = b$ ；③全等三角形对应边上的中线长相等；④相等的角是对顶角.其中真命题为（）

A、①③ B、②④ C、②③ D、①④

查看试题解析
4. 若函数 $y = k x (k \neq 0)$ 的图象过点 $P (- 1 ， 3)$ ，则该图象必过点（）

A、 $(1，3)$ B、 $(1，-3)$ C、 $(-3，1)$ D、 $(3，-1)$

查看试题解析
5. 已知点 $A (- 1 ， y_{1})$ ， $B (1.7 ， y_{2})$ 在函数 $y = - 9 x + b$ （b为常数）的图象上，则（）

A、 $y_{1} < y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} > 0 ， y_{2} < 0$ D、 $y_{1} = y_{2}$

查看试题解析
6. 解集在数轴上表示为如图所示的不等式组是（）

A、 ${\begin{array}{l} x > - 5 \\ x \geq 4 \end{array}$ B、 ${\begin{array}{l} x < - 5 \\ x \leq 4 \end{array}$ C、 ${\begin{array}{l} x < - 5 \\ x \geq 4 \end{array}$ D、 ${\begin{array}{l} x > - 5 \\ x \leq 4 \end{array}$

查看试题解析
7. 在 $△ A B C$ 中，若 $A B = 3, A C = \sqrt{2}, B C = \sqrt{7}$ ，则下列结论正确的是（）

A、 $∠ B = 90^{°}$ B、 $∠ C = 90^{°}$ C、 $△ A B C$ 是锐角三角形 D、 $△ A B C$ 是钝角三角形

查看试题解析
8. 若一次函数 $y = a x + b$ 的图象经过第一、二、四象限，则（）

A、 $a^{2} + b > 0$ B、 $a - b > 0$ C、 $a + b^{2} \geq 0$ D、 $a + b > 0$

查看试题解析
9. 把直线 $y = - x + 3$ 向上平移m个单位后，与直线 $y = 2x + 4$ 的交点在第一象限，则m的取值范围是（）

A、1＜m＜7 B、3＜m＜4 C、m＞1 D、m＜4

查看试题解析
10. 如图， $A B = A D$ ，点B关于 $A C$ 的对称点E恰好落在 $C D$ 上，若 $∠ B A D = α (0^{°} < α < 180^{°})$ ，则 $∠ A C B$ 的度数为（）

A、45° B、 $α - 45^{°}$ C、 $\frac{1}{2} α$ D、 $90^{°} - \frac{1}{2} α$

查看试题解析

二、填空题

11. 平面直角坐标系中，已知点 $A (a ， 3)$ ，点 $B (2 ， b)$ ，若线段 $A B$ 被y轴垂直平分，则 $a + b =$ .

查看试题解析
12. 在 $△ A B C$ 中， $A B = A C = 10$ ，底边上的高为6，则底边 $B C$ 为.

查看试题解析
13. 若一次函数 $y = k x + 3 (k \neq 0)$ 的图象向左平移4个单位后经过原点，则 $k =$ .

查看试题解析
14. 在 $R t △ A B C$ ， $C D$ 是斜边 $A B$ 上的中线， $∠ A D C = 80^{°}$ ，则 $∠ A =$ .

查看试题解析
15. 已知 $x - 2 y = 2$ ，且 $x > 1 ， y < 0$ ，设 $m = x + 2 y$ ，则m的取值范围是.

查看试题解析
16. 如图，P是等边 $△ A B C$ 外一点，把 $△ A B P$ 绕点B顺时针旋转60°到 $△ C B Q$ ，已知 $∠ A Q B = 150^{°}$ ， $Q A ： Q C = a ： b (b > a)$ ，则 $P B ： Q A =$ .（用含a，b的代数式表示）

查看试题解析
17. 在下列 $4 \times 4$ 网格中分别画出一个符合条件的直角三角形，要求三角形的顶点均在格点上，且满足：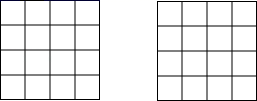

(1)、三边均为有理数；

(2)、其中只有一边为无理数.

查看试题解析
18. 若不等式 $3 (x - 2) + 5 < 4 (x - 1) + 6$ 的最小整数解为方程 $2 x - a x = 3$ 的解，求a的值.

查看试题解析
19. 如图， $△ A B C$ 中， $A B = A C$ ， $B G ， C F$ 分别是 $A C ， A B$ 边上的高线.
求证： $B G = C F$ .

查看试题解析
20. 在平面直角坐标系中，一次函数 $y = k x + b$ （k，b都是常数，且 $k \neq 0$ ），的图象经过点（1，0）和（0，3）.

(1)、求此函数的表达式.

(2)、已知点 $P (m ， n)$ 在该函数的图象上，且 $m + n = 4$ .
①求点P的坐标.

②若函数 $y = a x$ （a是常数，且 $a \neq 0$ ）的图象与函数 $y = k x + b$ 的图象相交于点P，写出不等式 $a x < k x + b$ 的解集.

查看试题解析
21. 如图，AD∥BC，∠A=90°，E是 $AB$ 上的一点，且 $A D = B E$ ， $∠ A E D = ∠ E C B$ .

(1)、判断 $△ D E C$ 的形状，并说明理由.

(2)、若 $A D = 3$ ， $A B = 9$ ，请求出 $C D$ 的长.

查看试题解析
22. 在平面直角坐标系中，有 $A (1, 2), B (3, 2)$ 两点，另有一次函数 $y = k x + b$ $(k \neq 0)$ 的图象.

(1)、若 $k = 1, b = 2$ ，判断函数 $y = k x + b$ $(k \neq 0)$ 的图象与线段 $A B$ 是否有交点？请说明理由.

(2)、当 $b = 12$ 时，函数 $y = k x + b$ $(k \neq 0)$ 图象与线段 $A B$ 有交点，求k的取值范围.

(3)、若 $b = - 2 k + 2$ ，求证：函数 $y = k x + b$ $(k \neq 0)$ 图象一定经过线段 $A B$ 的中点.

查看试题解析
23. 如图，在△ABC中，AB=AC ， D为直线BC上一动点（不与点B ， C重合），在AD的右侧作△ACE ，使得AE=AD ， ∠DAE=∠BAC ，连接CE ．

(1)、当D在线段 $B C$ 上时．
①求证： $△ B A D ≅ △ C A E$ ．

②请判断点D在何处时， $A C ⊥ D E$ ，并说明理由．

(2)、当 $C E / / A B$ 时，若 $△ A B D$ 中最小角为28°，求 $∠ A D B$ 的度数．

查看试题解析