初中数学北师大版九年级上学期期中模拟试卷(1~4单元)
试卷更新日期:2020-10-31 类型:期中考试
一、单选题
-
1. 下列说法:①一组对边平行且另一组对边相等的四边形是平行四边形;②两条对角线相等的四边形是矩形;③顺次连接菱形四边中点所得到的四边形是矩形;④四个角都相等的四边形是矩形;⑤平行四边形对角线的交点到一组对边的距离相等.正确的有( )个A、2 B、3 C、4 D、52. 如图,AC,BD是菱形ABCD的对角线,BH垂直AD于点H,若AC=4,BD=3,则BH的长为( )
 A、2.4 B、2.5 C、4.8 D、53. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x-1)=1035x2 C、x(x-1)=1035 D、2x(x+1)=10354. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒。若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( )
A、2.4 B、2.5 C、4.8 D、53. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x-1)=1035x2 C、x(x-1)=1035 D、2x(x+1)=10354. 如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒。若该无盖纸盒的底面积为600cm2 , 设剪去小正方形的边长为xcm,则可列方程为( ) A、
A、 B、
C、
B、
C、 D、
D、 5. 已知实数x1、x2满足x1+x2=4,x1x2=–3,则以x1、x2为根的一元二次方程是( )A、x2–4x–3=0 B、x2+4x–3=0 C、x2–4x+3=0 D、x2+4x+3=06. 如图,若DE∥FG∥BC , AD=DF=FB , 则S△ADE∶S四边形DFGE∶S四边形FBCG=( )
5. 已知实数x1、x2满足x1+x2=4,x1x2=–3,则以x1、x2为根的一元二次方程是( )A、x2–4x–3=0 B、x2+4x–3=0 C、x2–4x+3=0 D、x2+4x+3=06. 如图,若DE∥FG∥BC , AD=DF=FB , 则S△ADE∶S四边形DFGE∶S四边形FBCG=( )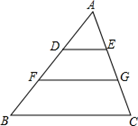 A、2∶6∶9 B、1∶3∶5 C、1∶3∶6 D、2∶5∶87. 如图,为估算学校的旗杆的高度,身高1.8米的小明同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m, BC=8m,则旗杆的高度是( )
A、2∶6∶9 B、1∶3∶5 C、1∶3∶6 D、2∶5∶87. 如图,为估算学校的旗杆的高度,身高1.8米的小明同学沿着旗杆在地面的影子AB由A向B走去,当她走到点C处时,她的影子的顶端正好与旗杆的影子的顶端重合,此时测得AC=2m, BC=8m,则旗杆的高度是( ) A、6.4m B、7m C、8m. D、9m8. 如图,直线a b c,AB= BC,若DF=9,则EF的长度为( )
A、6.4m B、7m C、8m. D、9m8. 如图,直线a b c,AB= BC,若DF=9,则EF的长度为( ) A、9 B、5 C、4 D、39. 如图,在矩形ABCD中, , ,过对角线交点 作 交AD于点E,交BC于点F,则DE的长是( )
A、9 B、5 C、4 D、39. 如图,在矩形ABCD中, , ,过对角线交点 作 交AD于点E,交BC于点F,则DE的长是( )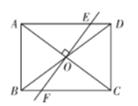 A、1 B、 C、2 D、10. 一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有71次摸到红球.请你估计这个口袋中白球的数量为( )个.A、29 B、30 C、3 D、7
A、1 B、 C、2 D、10. 一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有71次摸到红球.请你估计这个口袋中白球的数量为( )个.A、29 B、30 C、3 D、7二、填空题
-
11. 已知菱形 的一条对角线的长为 ,边 的长是 的一个根,则菱形 的周长为 .12. 如图,设四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,如此下去.则第2020个正方形的边长为.
 13. 如图,菱形 的边长为2, ,点Q是 的中点,点P是对角线 上一动点,则 最小值为.
13. 如图,菱形 的边长为2, ,点Q是 的中点,点P是对角线 上一动点,则 最小值为.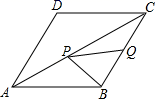 14. 如图,直线 与 轴、 轴分别相交于点A、B,点M在x轴上且不同于点A,点N是平面直角坐标系中的第一象限内任意一点.如果以A,B,M,N为顶点的四边形是菱形,那么满足条件的点M的坐标是.
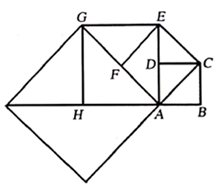
14. 如图,直线 与 轴、 轴分别相交于点A、B,点M在x轴上且不同于点A,点N是平面直角坐标系中的第一象限内任意一点.如果以A,B,M,N为顶点的四边形是菱形,那么满足条件的点M的坐标是.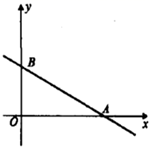 15. 已知 ,则 的值为 .16. 如图,已知 和 均是等边三角形,点 在同一条直线上, 与 交于点O, 与 交于点G, 与 交于点F,连接 ,则下列结论:① ;② ;③ ﹔④ ,其中正确结论有个.
15. 已知 ,则 的值为 .16. 如图,已知 和 均是等边三角形,点 在同一条直线上, 与 交于点O, 与 交于点G, 与 交于点F,连接 ,则下列结论:① ;② ;③ ﹔④ ,其中正确结论有个. 17. 如图,在长方形ABCD中,AB<BC,点P为长方形内部一点,过点P分别作PE⊥BC于点E、PF⊥CD于点F,分别以PF、CF为边作正方形PMNF,正方形GHCF,若两个正方形的面积之和为42,长方形PECF的面积为11,BE=DF=2,则长方形ABCD的面积为.
17. 如图,在长方形ABCD中,AB<BC,点P为长方形内部一点,过点P分别作PE⊥BC于点E、PF⊥CD于点F,分别以PF、CF为边作正方形PMNF,正方形GHCF,若两个正方形的面积之和为42,长方形PECF的面积为11,BE=DF=2,则长方形ABCD的面积为. 18. 如图,矩形 ABCD中,AB=8,AD=4,E在CD边上,且DE=2,将△ADE 沿直线AE 折叠,得到△AFE,连接 BF。则△ABF的面积为 .
18. 如图,矩形 ABCD中,AB=8,AD=4,E在CD边上,且DE=2,将△ADE 沿直线AE 折叠,得到△AFE,连接 BF。则△ABF的面积为 .
三、计算题
-
19. 已知 .(1)、求 的值;(2)、若 ,求x、y、z.20. 解方程:(1)、x2﹣2x﹣3=0;(2)、2x2+3x﹣1=0.
四、解答题
-
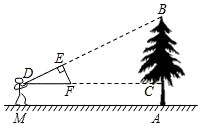
21. 如图,小明用自制的直角三角形纸板DEF测量树的高度AB . 他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm . EF=30cm , 测得边DF离地面的高度AC=1.5m , CD=10m , 求树高AB .
 22. 如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.求证:四边形BFDE是矩形;
22. 如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.求证:四边形BFDE是矩形; 23. 如图,已知△ABC , D是AC的中点,DE⊥AC于点D , 交AB于点E , 过点C作CF∥BA交ED的延长线于点F , 连接CE , AF . 求证:四边形AECF是菱形.
23. 如图,已知△ABC , D是AC的中点,DE⊥AC于点D , 交AB于点E , 过点C作CF∥BA交ED的延长线于点F , 连接CE , AF . 求证:四边形AECF是菱形. 24. 如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问P,Q两点从出发经过几秒时,点P,Q间的距离是10cm?
24. 如图,A,B,C,D为矩形的四个顶点,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向点B移动,点Q以2cm/s的速度向点D移动,当点P运动到点B停止时,点Q也随之停止运动,问P,Q两点从出发经过几秒时,点P,Q间的距离是10cm? 25. 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.
25. 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长. 26. 小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.
26. 小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.