初中数学人教版九年级上学期 第二十五章 25.2用列举法求概率
试卷更新日期：2020-10-30 类型：同步测试
一、单选题
-
1. 将一个篮球和一个足球随机放入三个不同的篮子中，则恰有一个篮子为空的概率为（ ）A、 B、 C、 D、2. 如图，随机闭合开关 ， ， 中的两个，则能让两盏灯泡同时发光的概率为（ ）
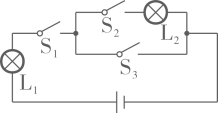A、 B、 C、 D、3. 一个不透明的袋子中装有1个红球，2个绿球，除颜色外无其他差别，从中随机摸出一个球，然后放回摇匀，再随机摸出一个，下列说法中，错误的是（ ）A、第一次摸出的球是红球，第二次摸出的球一定是绿球 B、第一次摸出的球是红球，第二次摸出的球不一定是绿球 C、第一次摸出的球是红球，第二次摸出的球不一定是红球 D、第一次摸出的球是红球的概率是 ；两次摸出的球都是红球的概率是4. 如图，有两个可以自由转动的转盘（每个转盘均被等分），同时转动这两个转盘，待转盘停止后，两个指针同时指在偶数上的概率是（ ）
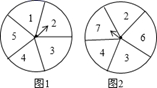A、 B、 C、 D、二、填空题
-
5. 两个人做游戏：每个人都从－1，0，1这三个整数中随机选择一个写在纸上，则两人所写整数的绝对值相等的概率为 ．6. 在如图所示的电路图中，当随机闭合开关 ， ， 中的两个时，能够让灯泡发光的概率为 ．
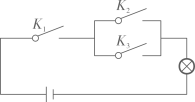7. A，B两个不透明的盒子里分别装有三张卡片，其中A盒里三张卡片上分别标有数字1，2，3，B盒里三张卡片上分别标有数字4，5，6，这些卡片除数字外其余都相同，将卡片充分摇匀.(1)、从A盒里班抽取一张卡、抽到的卡片上标有数字为奇数的概率是；(2)、从A盒，B盒里各随机抽取一张卡片，请用列表或画树状图的方法，求抽到的两张卡片上标有的数字之和大于7的概率.三、解答题
-
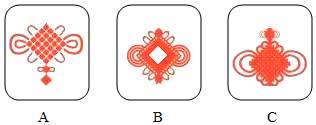
8. “中国结”是我国特有的手工编织工艺品，也是一种传统吉祥装饰物，如图，现有三张正面印有“中国结”图案的不透明卡片A，B，C，卡片除正面图案不同外，其余均相同．将三张卡片正面向下洗匀，小吉同学从中随机抽取一张卡片，记下图案后正面向下放回，洗匀后再从中随机抽取一张卡片．请用画树状图或列表的方法，求小吉同学抽出的两张卡片中含有A卡片的概率．
9. 现有三张不透明的卡片，其中两张卡片的正面图案为“神舟首飞”，第三张卡片的正面图案为“保卫和平”，卡片除正面图案不同外，其余均相同．将这三张卡片背面向上洗匀，从中随机抽取一张，记录图案后放回，重新洗匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求两次抽出的卡片上的图案都是“保卫和平”的概率．（图案为“神舟首飞”的两张卡片分别记为 、 ，图案为“保卫和平”的卡片记为B）
四、综合题
-
10. 小明、小亮和小强三人准备下象棋，他们约定用“抛硬币”的游戏方式来确定哪个人先下棋，规则如下：三人手中各持有一枚质地均匀的硬币，他们同时将手中硬币抛落到水平地面为一个回合，落地后，三枚硬币中，恰有两枚正面向上或者反面向上的两人先下棋；若三枚硬币均为正面向上或反面向上，则不能确定其中两人先下棋.(1)、请你完成下面表示游戏一个回合所有可能出现的结果的树状图；
解：树状图为：
(2)、求出一个回合能确定两人下棋的概率.11. 奥体中心为满足暑期学生对运动的需求，欲开设球类课程，该中心随机抽取部分学生进行问卷调查，被调查学生须从“羽毛球”、“篮球”、“足球”、“排球”、“乒乓球”中选择自己最喜欢的一项．根据调查结果绘制了不完整的条形统计图和扇形统计图，请根据图中信息，解答下列问题：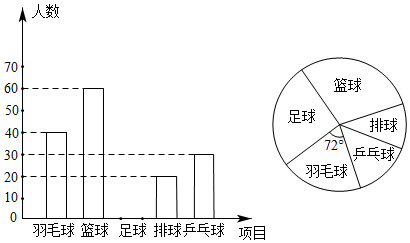
(1)、此次共调查了多少名学生？(2)、将条形统计图补充完整；(3)、我们把“羽毛球”“篮球”，“足球”、“排球”、“乒乓球”分别用A，B，C，D，E表示．小明和小亮分别从这些项目中任选一项进行训练，利用树状图或表格求出他俩选择不同项目的概率．12. 将4张印有“梅”“兰”“竹”“菊”字样的卡片（卡片的形状、大小、质地都相同）放在一个不透明的盒子中，将卡片搅匀.(1)、从盒子中任意取出1张卡片，恰好取出印有“兰”字的卡片的概率为.(2)、先从盒子中任意取出1张卡片，记录后放回并搅匀，再从中任意取出1张卡片，求取出的两张卡片中，至少有1张印有“兰”字的概率（请用画树状图或列表等方法求解）.13. 为了更好地解决养老问题，某服务中心引入优质社会资源为甲，乙两个社区共30名老人提供居家养老服务，收集得到这30名老人的年龄（单位：岁）如下：甲社区
67
68
73
75
76
78
80
82
83
84
85
85
90
92
95
乙社区
66
69
72
74
75
78
80
81
85
85
88
89
91
96
98
根据以上信息解答下列问题：
(1)、求甲社区老人年龄的中位数和众数；(2)、现从两个社区年龄在70岁以下的4名老人中随机抽取2名了解居家养老服务情况，求这2名老人恰好来自同一个社区的概率．