初中数学人教版九年级上学期 第二十四章测试卷
试卷更新日期:2020-10-30 类型:单元试卷
一、单选题
-
1. 已知⊙O的半径为1,弦AB长为1,则弦AB所对的圆周角为( )A、60° B、30° C、60°和120° D、30°和150°2. 在圆内接正方形ABCD中,正方形的边长AB是8,则这个正方形的中心角和边心距是( )A、90°,4 B、90°,1 C、45°,4 D、45°,13. 如图所示,在半径为10cm的⊙O中,弦AB=16cm , OC⊥AB于点C , 则OC等于( )
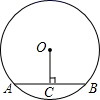 A、3cm B、4cm C、5cm D、6cm4. 如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )
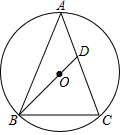
A、3cm B、4cm C、5cm D、6cm4. 如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )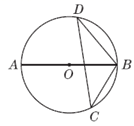 A、60° B、50° C、40° D、30°5. 如图,在 中, ,点O为 的内心,则 的度数为( )
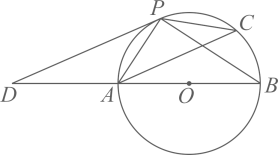
A、60° B、50° C、40° D、30°5. 如图,在 中, ,点O为 的内心,则 的度数为( )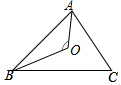 A、 B、 C、 D、6. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
A、 B、 C、 D、6. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )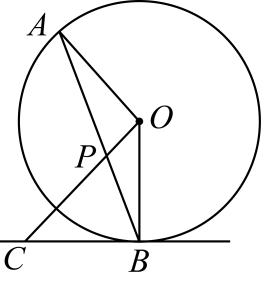 A、 B、 C、 D、7. 如图, 与正六边形 的边 分别交于点 ,点M为劣弧 的中点.若 .则点O到 的距离是( )
A、 B、 C、 D、7. 如图, 与正六边形 的边 分别交于点 ,点M为劣弧 的中点.若 .则点O到 的距离是( )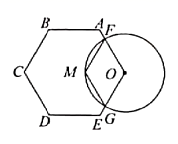 A、4 B、 C、 D、8. 已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为( )
A、4 B、 C、 D、8. 已知⊙O是正六边形ABCDEF的外接圆,P为⊙O上除C、D外任意一点,则∠CPD的度数为( )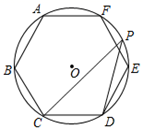 A、30° B、30°或150° C、60° D、60°或120°
A、30° B、30°或150° C、60° D、60°或120°二、填空题
-
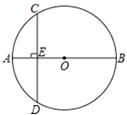
9. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE =1:3,则AB=.
 10. 如图,AB是 的直径,点C,D,E都在 上,∠1=55°,则∠2=°
10. 如图,AB是 的直径,点C,D,E都在 上,∠1=55°,则∠2=°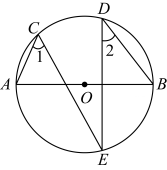 11. 如图,在 中, 的半径为1,点P是 边上的动点,过点P作 的一条切线 (其中点Q为切点),则线段 长度的最小值为 .
11. 如图,在 中, 的半径为1,点P是 边上的动点,过点P作 的一条切线 (其中点Q为切点),则线段 长度的最小值为 .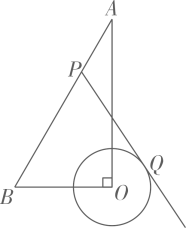 12. 我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积 来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积 来近似估计半径为1的⊙O的面积,则 .(结果保留根号)
12. 我国魏晋时期著名的数学家刘徽在《九章算术》中提出了“割圆术——割之弥细,所失弥少,隔之又割,以至不可割,则与圆周合体,而无所失也.”也就是利用圆的内接多边形逐步逼近圆的方法来近似计算圆的面积和周长.如图1,若用圆的内接正六边形的面积 来近似估计半径为1的⊙O的面积,再用如图2的圆的内接正十二边形的面积 来近似估计半径为1的⊙O的面积,则 .(结果保留根号)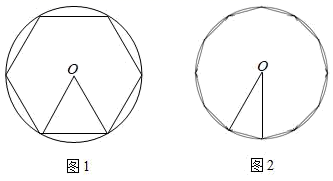 13. 如图,在边长为3的正六边形ABCDEF中,将四边形ADEF绕顶点A顺时针旋转到四边形AD'E'F′处,此时边AD′与对角线AC重叠,则图中阴影部分的面积是.
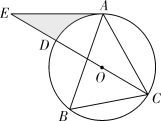
13. 如图,在边长为3的正六边形ABCDEF中,将四边形ADEF绕顶点A顺时针旋转到四边形AD'E'F′处,此时边AD′与对角线AC重叠,则图中阴影部分的面积是. 14. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .
14. 如图,点C、D分别是半圆AOB上的三等分点,若阴影部分的面积为 ,则半圆的半径OA的长为 .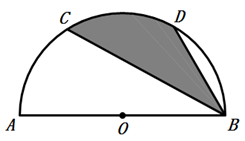
三、综合题
-
15. 如图,四边形ABCD中,AB∥CD,点O在BD上,以O为圆心的圆恰好经过A、B、C三点,⊙O交BD于E,交AD于F,且弧AE=弧CE,连接OA、OF.
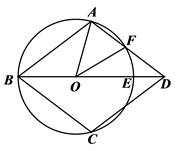 (1)、求证:四边形ABCD是菱形;(2)、若∠AOF=3∠FOE,求∠ABC的度数.16. 如图, 在平面直角坐标系中,顶点的坐标分别为 , , .
(1)、求证:四边形ABCD是菱形;(2)、若∠AOF=3∠FOE,求∠ABC的度数.16. 如图, 在平面直角坐标系中,顶点的坐标分别为 , , . (1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).17. 如图,⊙O的半径OA 弧BC于E,D是⊙O上一点.
(1)、画出与 关于y轴对称的 ;(2)、将 绕点 顺时针旋转90°得到 , 弧是点A所经过的路径,则旋转中心 的坐标为.(3)、求图中阴影部分的面积(结果保留 ).17. 如图,⊙O的半径OA 弧BC于E,D是⊙O上一点. (1)、求证: ;(2)、若AE=2,BC=6,求OA的长.
(1)、求证: ;(2)、若AE=2,BC=6,求OA的长.