初中数学人教版九年级上学期 第二十四章 24.3正多边形和圆
试卷更新日期:2020-10-30 类型:同步测试
一、单选题
-
1. 若一个正多边形的内角和为1800°,则这个正多边形的一个外角为( )A、 B、 C、 D、2. 下列说法中正确的是( )A、平分弦的直径平分弦所对的弧 B、圆内接正六边形,一条边所对的圆周角是30° C、相等的圆周角所对的弧也相等 D、若两条平行直线被一个圆截得的线段长度相等,则圆心到这两条直线的距离相等3. 下列命题①若a>b,则ac>bc;②若a=1,则 =a;③ 的平方根是 ④各边都相等的多边形是正多边形,其中真命题的个数是( )A、0 B、1 C、2 D、34. 将每一个内角都是108°的五边形按如图所示方式放置,若直线m∥n , 则下列结论中一定正确的是( )
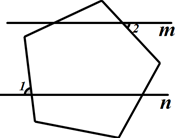 A、∠1=∠2+36° B、∠1=∠2+72° C、∠1+∠2=90° D、2∠1+∠2=180°5. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A、∠1=∠2+36° B、∠1=∠2+72° C、∠1+∠2=90° D、2∠1+∠2=180°5. 如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )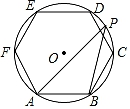 A、15° B、30° C、45° D、60°6. 如图, 与正六边形 的边 分别交于点 ,点M为劣弧 的中点.若 .则点O到 的距离是( )
A、15° B、30° C、45° D、60°6. 如图, 与正六边形 的边 分别交于点 ,点M为劣弧 的中点.若 .则点O到 的距离是( )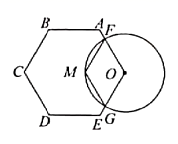 A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题
-
7. 如图,▱BCDE的顶点B、C、D在半圆O上,顶点E在直径AB上,连接AD,若∠CDE=68°,则∠ADE的度数为°.
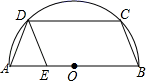 8. 如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 ,则 的度数是.
8. 如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 ,则 的度数是. 9. 若一个正多边形的每一个外角都是40°,则这个正多边形的内角和等于 .10. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.
9. 若一个正多边形的每一个外角都是40°,则这个正多边形的内角和等于 .10. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.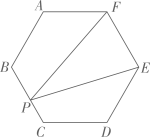 11. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
11. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .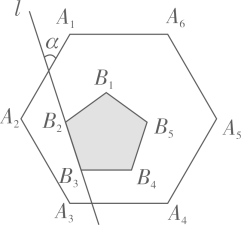 12. 一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则 度.
12. 一个蜘蛛网如图所示,若多边形ABCDEFGHI为正九边形,其中心点为点O,点M、N分别在射线OA、OC上,则 度.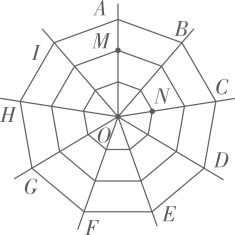
三、解答题
-
13. 如图, 是 的内接正五边形.求证: .
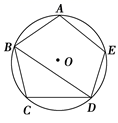 14. 如图,在网格纸中,O、A都是格点,以O为圆心, 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
14. 如图,在网格纸中,O、A都是格点,以O为圆心, 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)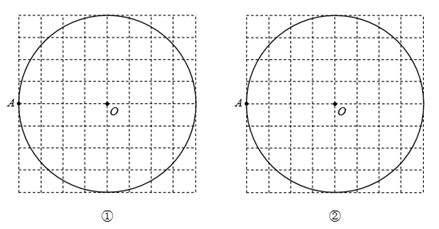 (1)、在圆①中画圆O的一个内接正六边形 ;(2)、在图②中画圆O的一个内接正八边形 .
(1)、在圆①中画圆O的一个内接正六边形 ;(2)、在图②中画圆O的一个内接正八边形 .四、综合题

