初中数学北师大版八年级上学期 第七章 7.3平行线的判定
试卷更新日期:2020-10-30 类型:同步测试
一、单选题
-
1. 如图,直线
 被直线
被直线 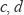 所截下列条件能判定
所截下列条件能判定  的是( )
的是( )  A、
A、 B、
B、 C、
C、 D、
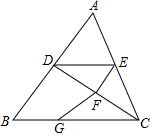
D、 2. 如图,已知 ,则图中互相平行的线段是( )
2. 如图,已知 ,则图中互相平行的线段是( )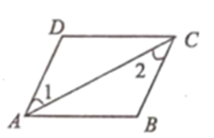 A、AB//CD B、AD//BC C、AB//CD或AD//BC D、AB//CD且AD//BC3. 下图给出了过直线外一点作已知直线的平行线的一种方法,其依据是( )
A、AB//CD B、AD//BC C、AB//CD或AD//BC D、AB//CD且AD//BC3. 下图给出了过直线外一点作已知直线的平行线的一种方法,其依据是( ) A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、平行于同一直线的两条直线平行4. 如图,下列条件中不能判断直线 与直线 平行的是( ).
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、平行于同一直线的两条直线平行4. 如图,下列条件中不能判断直线 与直线 平行的是( ).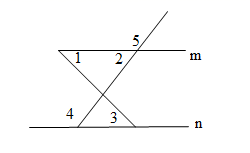 A、 B、 C、 D、5. 如图,已知∠1=∠2=∠3=55°,那么∠4的度数是( )
A、 B、 C、 D、5. 如图,已知∠1=∠2=∠3=55°,那么∠4的度数是( ) A、55° B、115° C、120° D、125°6. 如图,△ ≌△ ,那么下列结论错误的是( )
A、55° B、115° C、120° D、125°6. 如图,△ ≌△ ,那么下列结论错误的是( ) A、 B、 C、 ∥ D、 ∥
A、 B、 C、 ∥ D、 ∥二、填空题
-
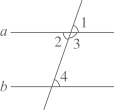
7. 如图,请填写一个条件,使结论成立:∵ , ∴ .
 8. 如图,将两个含角 的直角三角板的最长边靠在一起滑动,可知直角 边,依据是.
8. 如图,将两个含角 的直角三角板的最长边靠在一起滑动,可知直角 边,依据是.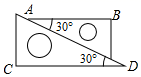
三、综合题
-
9. 完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.

求证:BE∥DF.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴+∠C=180°.
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1= ∠ABC.
同理,∠2= ∠ADC.
∴∠1=∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )