安徽省六安市舒城县2019-2020学年高一上学期数学期末考试试卷
试卷更新日期:2020-10-30 类型:期末考试
一、单选题
-
1. 已知集合 ,则 ( )A、[0,1] B、[0,1) C、(0,1 ] D、(0,1)2. 函数 的定义域为( )A、 B、 C、 D、3. 下列函数中,既是偶函数又在 上单调递增的函数是( )A、 B、 C、 D、4. 把函数 图象上各点的横坐标缩短到原来的 倍(纵坐标不变),再将图象向右平移 个单位,得到函数 ,那么 的值为( )A、 B、 C、 D、5. 若 =2,则sinθcosθ的值是( )A、- B、 C、± D、6. 若 ,则( )A、 B、 C、 D、7. 函数 的值域为( )A、 B、 C、 D、8. 已知 是定义在R上的周期为2的函数,当 时, ,则 的值为( )A、2 B、-1 C、 D、19. 函数f(x)= 在[- , ]。的图像大致为( )A、
 B、
B、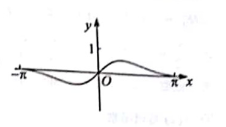 C、
C、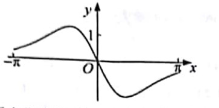 D、
D、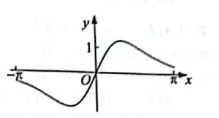 10. 关于函数 有下述四个结论:
10. 关于函数 有下述四个结论:①f(x)是偶函数②f(x)在区间( , )单调递增③f(x)在 有4个零点④f(x)的最大值为2其中所有正确结论的编号是( )
A、①②④ B、②④ C、①④ D、①③11. 同时具备以下性质:“①最小周期是 ;②图象关于直线 对称;③在 上是增函数;④一个对称中心为 ”的一个函数是( )A、 B、 C、 D、12. 定义域为R的函数 若函数 有且只有3个不同的零点 , , ,则 的值为( )A、6 B、ln6 C、3ln2 D、3ln313. 函数 的零点是( )A、 B、 和 C、1 D、1和-114. 若不等式 对任意的 恒成立,则实数 的取值范围是( )A、(-∞,0] B、(-∞, ] C、[0,+∞) D、[ ,+∞)15. 函数 在 为减函数,则a的取值范围是( )A、 B、 C、 D、二、填空题
-
16. 函数y=tan( + ),x∈(0, ]的值域是 .17. 已知 是奇函数,且当 时, ,则 .18. 已知偶函数 在区间 单调递增,则满足 的x取值范围是.19. 已知函数 ,若实数 互不相等,且满足 ,则 的取值范围是.20. 已知函数 为奇函数,则 .
三、解答题
-
21. 已知角 终边上的一点 ,( ).(1)、求 的值;(2)、求 的值.22. 已知幂函数 在 上单调递增,函数 ;(1)、求m的值;(2)、当 时,记 、 的值域分别是A、B,若 ,求实数k的取值范围;23. 已知函数 , .(1)、求函数 的值域;(2)、设 ,若 的图像恒在x轴上方,求a的范围.24. 已知函数 ( , , )的部分图象如下图所示.
 (1)、求 的解析式;(2)、求函数 在 的单调减区间.25. 某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气 后,测得车库内的一氧化碳浓度为 ,继续排气 ,又测得浓度为 ,经检测知该地下车库一氧化碳浓度 与排气时间 存在函数关系: ( , 为常数).(1)、求 , 的值;(2)、若地下车库中一氧化碳浓度不高于 为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?26. 2018年1月8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当 时,y是x的二次函数;当 时, 测得数据如下表(部分):
(1)、求 的解析式;(2)、求函数 在 的单调减区间.25. 某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气 后,测得车库内的一氧化碳浓度为 ,继续排气 ,又测得浓度为 ,经检测知该地下车库一氧化碳浓度 与排气时间 存在函数关系: ( , 为常数).(1)、求 , 的值;(2)、若地下车库中一氧化碳浓度不高于 为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?26. 2018年1月8日,中共中央、国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当 时,y是x的二次函数;当 时, 测得数据如下表(部分):x(单位:克)
0
1
2
9
…
y
0
3
…
(1)、求y关于x的函数关系式 ;(2)、当该产品中的新材料含量x为何值时,产品的性能指标值最大.