上海市普陀区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-30 类型:期末考试
一、单选题
-
1. 已知 ,那么下列等式中,不一定正确的是( )A、 B、 C、 D、2. 下列二次函数中,如果函数图象的对称轴是 轴,那么这个函数是( )A、 B、 C、 D、3. 已知在 中, , ,那么下列说法中正确的是( )A、 B、 C、 D、4. 下列说法中,正确的是( )A、如果k=0, 是非零向量,那么k =0 B、如果 是单位向量,那么 =1 C、如果| |=| |,那么 = 或 =﹣ D、已知非零向量 ,如果向量 =﹣5 ,那么 ∥5. 如果二次函数 的图像如图所示,那么一次函数 的图像经过( )
 A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限6. 如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果 ,AD=9,那么BC的长是( )
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限6. 如图,在Rt△ABC中,∠ACB=90°, CD⊥AB,垂足为点D,如果 ,AD=9,那么BC的长是( )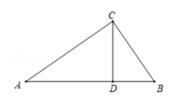 A、4 B、6 C、2 D、3
A、4 B、6 C、2 D、3二、填空题
-
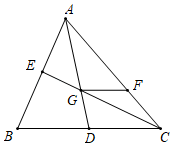
7. 化简: .8. 抛物线 在对称轴左侧的部分是上升的,那么 的取值范围是.9. 已知函数 ,如果 ,那么 .10. 如果抛物线 与 轴的一个交点的坐标是 ,那么与 轴的另一个交点的坐标是.11. 将二次函数 的图像向下平移 个单位后,它的顶点恰好落在 轴上,那么 的值等于.12. 已知在 中, , , ,那么 .13. 如图,△ABC的中线AD、CE交于点G,点F在边AC上,GF∥BC,那么 的值是.
 14. 如图,在 与 中, ,要使 与 相似,还需添加一个条件,这个条件可以是(只需填一个条件)
14. 如图,在 与 中, ,要使 与 相似,还需添加一个条件,这个条件可以是(只需填一个条件) 15. 如图,在 中, , 是三角形的角平分线,如果 , ,那么点 到直线 的距离等于.
15. 如图,在 中, , 是三角形的角平分线,如果 , ,那么点 到直线 的距离等于. 16. 如图,斜坡 长为100米,坡角 ,现因“改小坡度”工程的需要,将斜坡 改造成坡度 的斜坡 ( 、 、 三点在地面的同一条垂线上),那么由点 到点 下降了米(结果保留根号)
16. 如图,斜坡 长为100米,坡角 ,现因“改小坡度”工程的需要,将斜坡 改造成坡度 的斜坡 ( 、 、 三点在地面的同一条垂线上),那么由点 到点 下降了米(结果保留根号) 17. 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O , AO=CO , CD⊥BD , 如果CD=3,BC=5,那么AB= .
17. 如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O , AO=CO , CD⊥BD , 如果CD=3,BC=5,那么AB= . 18. 如图,在 中, , , ,点 为边 上一点, ,将 绕点 旋转得到 (点 、 、 分别与点 、 、 对应),使 ,边 与边 交于点 ,那么 的长等于.
18. 如图,在 中, , , ,点 为边 上一点, ,将 绕点 旋转得到 (点 、 、 分别与点 、 、 对应),使 ,边 与边 交于点 ,那么 的长等于.
三、解答题
-
19. 计算:20. 如图,在 中,点 、 、 分别在边 、 、 上, , , .
 (1)、当 时,求 的长;(2)、设 , ,那么 , (用向量 , 表示)21. 如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P, .
(1)、当 时,求 的长;(2)、设 , ,那么 , (用向量 , 表示)21. 如图,在△ABC中,点P、D分别在边BC、AC上,PA⊥AB,垂足为点A,DP⊥BC,垂足为点P, . (1)、求证:∠APD=∠C;(2)、如果AB=3,DC=2,求AP的长.22. 函数 与函数 ( 、 为不等于零的常数)的图像有一个公共点 ,其中正比例函数 的值随 的值增大而减小,求这两个函数的解析式.23. 已知:如图,四边形 的对角线 、 相交于点 , .
(1)、求证:∠APD=∠C;(2)、如果AB=3,DC=2,求AP的长.22. 函数 与函数 ( 、 为不等于零的常数)的图像有一个公共点 ,其中正比例函数 的值随 的值增大而减小,求这两个函数的解析式.23. 已知:如图,四边形 的对角线 、 相交于点 , . (1)、求证: ;(2)、设 的面积为 , ,求证:S四边形ABCD .24. 在平面直角坐标系 中(如图),已知抛物线 经过点 ,与 轴交于点 ,抛物线的顶点为点 ,对称轴与 轴交于点 .
(1)、求证: ;(2)、设 的面积为 , ,求证:S四边形ABCD .24. 在平面直角坐标系 中(如图),已知抛物线 经过点 ,与 轴交于点 ,抛物线的顶点为点 ,对称轴与 轴交于点 . (1)、求抛物线的表达式及点 的坐标;(2)、点 是 轴正半轴上的一点,如果 ,求点 的坐标;(3)、在(2)的条件下,点 是位于 轴左侧抛物线上的一点,如果 是以 为直角边的直角三角形,求点 的坐标.25. 如图,在梯形 中, , , , , ,点 在边 上, ,点 是射线 上一个动点(不与点 、 重合),联结 交射线 于点 ,设 , .
(1)、求抛物线的表达式及点 的坐标;(2)、点 是 轴正半轴上的一点,如果 ,求点 的坐标;(3)、在(2)的条件下,点 是位于 轴左侧抛物线上的一点,如果 是以 为直角边的直角三角形,求点 的坐标.25. 如图,在梯形 中, , , , , ,点 在边 上, ,点 是射线 上一个动点(不与点 、 重合),联结 交射线 于点 ,设 , .
 (1)、求 的长;(2)、当动点 在线段 上时,试求 与 之间的函数解析式,并写出函数的定义域;(3)、当动点 运动时,直线 与直线 的夹角等于 ,请直接写出这时线段 的长.
(1)、求 的长;(2)、当动点 在线段 上时,试求 与 之间的函数解析式,并写出函数的定义域;(3)、当动点 运动时,直线 与直线 的夹角等于 ,请直接写出这时线段 的长.