上海市闵行区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-10-30 类型：期末考试

进入出卷网下载

一、单选题

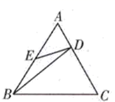
1. 如果把Rt△ABC的各边长都扩大到原来的n倍，那么锐角A的四个三角比值（）

A、都缩小到原来的n倍 B、都扩大到原来的n倍； C、都没有变化 D、不同三角比的变化不一致.

查看试题解析
2. 已知P是线段AB的黄金分割点，且AP>BP，那么下列比例式能成立的是（）

A、 $\frac{A B}{A P} = \frac{A P}{B P}$ B、 $\frac{A B}{A P} = \frac{B P}{A B}$ C、 $\frac{B P}{A P} = \frac{A B}{B P}$ D、 $\frac{A B}{A P} = \frac{\sqrt{5} - 1}{2}$

查看试题解析
3. k为任意实数，抛物线 $y = a {(x - k)}^{2} - k （ a \neq 0 ）$ 的顶点总在（）

A、直线 $y = x$ 上 B、直线 $y = - x$ 上 C、x轴上 D、y轴上

查看试题解析
4. 如图，在正三角形 $A B C$ 中，分别在 $A C$ ， $A B$ 上，且 $\frac{A D}{A C} = \frac{1}{3}$ ， $A E = B E$ ，则有（）

A、 $Δ A E D ∽ Δ B E D$ B、 $Δ A E D ∽ Δ C B D$ C、 $Δ A E D ∽ Δ A B D$ D、 $Δ B A D ∽ Δ B C D$

查看试题解析
5. 下列命题是真命题的是（）

A、经过平面内任意三点可作一个圆 B、相等的圆心角所对的弧一定相等 C、相交两圆的公共弦一定垂直于两圆的连心线 D、内切两圆的圆心距等于两圆的半径的和

查看试题解析
6. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像如图所示，现有以下结论：① $a < 0$ ；② $a b c > 0$ ；③ $a - b + c < 0$ ；④ $b^{2} - 4 a c < 0$ ；其中正确的结论有（）

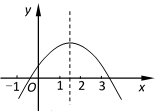A、1个 B、2个 C、3个 D、4个.

查看试题解析

二、填空题

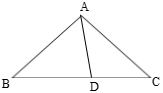
7. 已知线段a=4，c=9，那么a和c的比例中项b= ．

查看试题解析
8. 在 $△ ABC$ 中，若 $∠ C = 90^{\circ}$ ， $AB = 10$ ， $sinA = \frac{2}{5}$ ，则 $BC =$

查看试题解析
9. 抛物线 $y = - 2 {(x - 1)}^{2} + 3$ 在对称轴右侧的部分是的.(填“上升”或“下降”)

查看试题解析
10. 如果两个相似三角形的相似比为2︰3，两个三角形的周长的和是100cm，那么较小的三角形的周长为cm.

查看试题解析
11. $\vec{e}$ 为单位向量， $\vec{a}$ 与 $\vec{e}$ 的方向相反，且长度为6，那么 $\vec{a}$ = $\vec{e}$ .

查看试题解析
12. 某人从地面沿着坡度为 $i = 1 : \sqrt{3}$ 的山坡走了 $100$ 米，这时他离地面的高度是米．

查看试题解析
13. 已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在BC的延长线上的点E处，那么 $\tan ∠ B A E$ =.

查看试题解析
14. 已知在Rt△ABC中，∠C=90º，AC=3，BC=4，⊙C与斜边AB相切，那么⊙C的半径为.

查看试题解析
15. 设抛物线l： $y = a x^{2} + b x + c (a \neq 0)$ 的顶点为D，与y轴的交点是C，我们称以C为顶点，且过点D的抛物线为抛物线l的“伴随抛物线”，请写出抛物线 $y = x^{2} - 4 x + 1$ 的伴随抛物线的解析式.

查看试题解析
16. 半径分别为3cm与 $\sqrt{17}$ cm的⊙O₁与⊙O₂相交于A、B两点，如果公共弦AB= $4 \sqrt{2}$ cm，那么圆心距O₁O₂的长为cm.

查看试题解析
17. 正五边形的边长与边心距的比值为.(用含三角比的代数式表示)

查看试题解析
18. 如图，在等腰△ABC中，AB=AC=4，BC=6点D在底边BC上，且∠DAC=∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为.

查看试题解析

三、解答题

19. 已知二次函数图象的最高点是A(1，4)，且经过点B(0，3)，与 $x$ 轴交于C、D两点(点C在点D的左侧).求△BCD的面积.

查看试题解析
20. 已知：在平行四边形ABCD中，AB︰BC=3︰2.

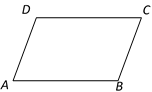(1)、根据条件画图：作∠BCD的平分线，交边AB于点E，取线段BE的中点F，连接DF交CE于点G.

(2)、设 $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b}$ ，那么向量 $\vec{C G}$ =.(用向量 $\vec{a}$ 、 $\vec{b}$ 表示)，并在图中画出向量 $\vec{D G}$ 在向量 $\vec{A B}$ 和 $\vec{A D}$ 方向上的分向量.

查看试题解析
21. 如图，梯形ABCD中，AD∥BC，∠ADC=90º，AD= 2，BC= 4， $\tan B = 3$ .以AB为直径作⊙O，交边DC于E、F两点.

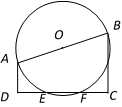(1)、求证：DE=CF.

(2)、求直径AB的长.

查看试题解析
22. 2019年第18号台风“米娜”于9月29日早晨5点整，由位于台湾省周边的B岛东南方约980千米的西北太平洋洋面上(A点)生成，向西北方向移动.并于9月30日20时30分到达B岛后风力增强且转向，一路向北于24小时后在浙江省舟山市登陆.“米娜”在登录后风力减弱且再一次转向，以每小时20千米的速度向北偏东30º的方向移动，距台风中心170千米的范围内是受台风影响的区域.已知上海位于舟山市北偏西7º方向，且距舟山市250千米.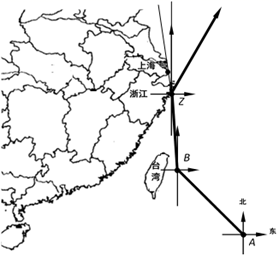

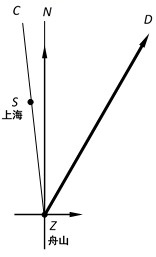(1)、台风中心从生成点(A点)到达B岛的速度是每小时多少千米？

(2)、10月2日上海受到“米娜”影响，那么上海遭受这次台风影响的时间有多长？(结果保留整数，参考数据： $\sin 23^{\circ} \approx 0.39$ ， $\cos 23^{\circ} \approx 0.92$ ， $\tan 23^{\circ} \approx 0.42$ ； $\sin 37^{\circ} \approx 0.60$ ， $\cos 37^{\circ} \approx 0.80$ ， $\tan 37^{\circ} \approx 0.75$ .)

查看试题解析
23. 如图，在△ABC中，BD是AC边上的高，点E在边AB上，联结CE交BD于点O，且 $A D \cdot O C = A B \cdot O D$ ，AF是∠BAC的平分线，交BC于点F，交DE于点G.

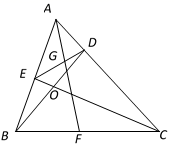(1)、求证：CE⊥AB．

(2)、求证： $A F \cdot D E = A G \cdot B C$ .

查看试题解析
24. 已知：在平面直角坐标系xOy中，对称轴为直线x = -2的抛物线经过点C(0，2)，与x轴交于A(-3，0)、B两点(点A在点B的左侧).

(1)、求这条抛物线的表达式.

(2)、连接BC，求∠BCO的余切值.

(3)、如果过点C的直线，交x轴于点E，交抛物线于点P，且∠CEO =∠BCO，求点P的坐标.

查看试题解析
25. 已知：如图，在Rt△ABC和Rt△ACD中，AC=BC，∠ACB=90°，∠ADC=90°，CD=2，(点A、B分别在直线CD的左右两侧)，射线CD交边AB于点E，点G是Rt△ABC的重心，射线CG交边AB于点F，AD=x，CE=y.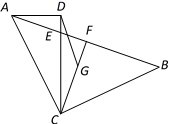

(1)、求证：∠DAB=∠DCF.

(2)、当点E在边CD上时，求y关于x的函数关系式，并写出x的取值范围.

(3)、如果△CDG是以CG为腰的等腰三角形，试求AD的长.

查看试题解析