黑龙江省齐齐哈尔市铁锋区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-29 类型:期末考试
一、单选题
-
1. 抛物线y=(x﹣1)2+2的对称轴为( )A、直线x=1 B、直线x=﹣1 C、直线x=2 D、直线x=﹣22. 下列事件中,是必然事件的是( )A、从装有10个黑球的不透明袋子中摸出一个球,恰好是红球 B、抛掷一枚普通正方体骰子,所得点数小于7 C、抛掷一枚一元硬币,正面朝上 D、从一副没有大小王的扑克牌中抽出一张,恰好是方块3. 已知反比例函数y= 的图象上有A(x1 , y1)、B(x2 , y2)两点,当x1<x2<0时,y1<y2 , 则m的取值范围是( )
A、m<0 B、m>0 C、m< D、m>4. 用配方法解一元二次方程ax2+bx+c=0(a≠0),此方程可变形为( )A、 B、 C、 D、5.如图,将正方形图案绕中心O旋转180°后,得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、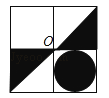 6. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( )
6. 如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不一定相似的是( ) A、
A、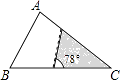 B、
B、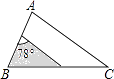 C、
C、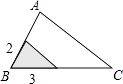 D、
D、 7. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
7. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )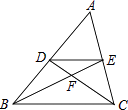 A、 = B、 C、 D、8.
A、 = B、 C、 D、8.如图,已知A,B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
 A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )
9. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )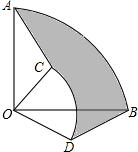 A、 B、
A、 B、 C、
C、 D、
D、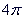 10. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣ ,结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大:④若m , n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2;⑤ <0,其中正确的结论有( )
10. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3,0),其对称轴为直线x=﹣ ,结合图象分析下列结论:①abc>0;②3a+c>0;③当x<0时,y随x的增大而增大:④若m , n(m<n)为方程a(x+3)(x﹣2)+3=0的两个根,则m<﹣3且n>2;⑤ <0,其中正确的结论有( )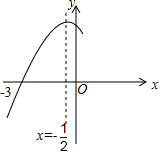 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 若抛物线y=2x2+6x+m与x轴有两个交点,则m的取值范围是 .12. 在一个暗箱里放有m个除颜色外其他完全相同的小球,这m个小球中红球只有4个,每次将球搅匀后,任意摸出一个球记下颜色再放回暗箱.通过大量重复摸球试验后发现,摸到红球的频率稳定在25%,那么可以推算m大约是.13. 如图,是一个半径为6cm , 面积为12πcm2的扇形纸片,现需要一个半径为R的圆形纸片,使两张纸片刚好能组合成圆锥体,则R等于cm .
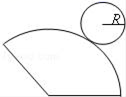 14. 如图,AB是⊙O的直径,AB=6,点C在⊙O上,∠CAB=30°,D为 的中点,P是直径AB上一动点,则PC+PD的最小值为 .
14. 如图,AB是⊙O的直径,AB=6,点C在⊙O上,∠CAB=30°,D为 的中点,P是直径AB上一动点,则PC+PD的最小值为 . 15. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是 .16.
15. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是 .16.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
 17. 如图,点 、 、 …在反比例函数 的图象上,点 、 、 ……在反比例函数 的图象上, ,且 ,则 ( 为正整数)的纵坐标为 . (用含 的式子表示)
17. 如图,点 、 、 …在反比例函数 的图象上,点 、 、 ……在反比例函数 的图象上, ,且 ,则 ( 为正整数)的纵坐标为 . (用含 的式子表示)
三、解答题
-
18. 解方程:(1)、x2﹣4x+2=0;(2)、19. 爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字﹣1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为 .(1)、请你帮他们用树状图或列表法表示 所有可能出现的结果;(2)、求满足关于x的方程 没有实数根的概率.20. 如图,已知A(﹣4,0),B(0,4),现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C .
 (1)、求C点坐标及直线BC的解析式:(2)、点P从点A开始以每秒2个单位长度的速度匀速沿着x轴向右运动,若运动时间用t秒表示.△BCP的面积用S表示,请你直接写出S与t的函数关系.21. 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D , 且AC平分∠DAB . 延长DC交AB的延长线于点P .
(1)、求C点坐标及直线BC的解析式:(2)、点P从点A开始以每秒2个单位长度的速度匀速沿着x轴向右运动,若运动时间用t秒表示.△BCP的面积用S表示,请你直接写出S与t的函数关系.21. 如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D , 且AC平分∠DAB . 延长DC交AB的延长线于点P . (1)、求证:PC2=PA•PB;(2)、若3AC=4BC , ⊙O的直径为7,求线段PC的长.22. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20C时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)、求证:PC2=PA•PB;(2)、若3AC=4BC , ⊙O的直径为7,求线段PC的长.22. 小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20C时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题: (1)、当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小明上午八点将饮水机在通电开机(此时饮水机中原有水的温度为20℃后即外出散步,预计上午八点半散步回到家中,回到家时,他能喝到饮水机内不低于30℃的水吗?请说明你的理由.23. 综合与实践
(1)、当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;(2)、求图中t的值;(3)、若小明上午八点将饮水机在通电开机(此时饮水机中原有水的温度为20℃后即外出散步,预计上午八点半散步回到家中,回到家时,他能喝到饮水机内不低于30℃的水吗?请说明你的理由.23. 综合与实践背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D , E分别是边BC , AC的中点,连接DE , 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
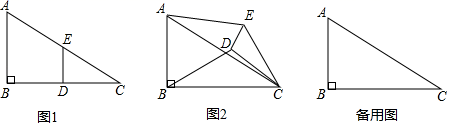
问题解决:
(1)、①当α=0°时, =;②当α=180°时, = .(2)、试判断:当0°≤a<360°时, 的大小有无变化?请仅就图2的情形给出证明.(3)、当△EDC旋转至A , D , E三点共线时,求得线段BD的长为 .24. 综合与探究如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣3,0)、B两点,与y轴相交于点 .当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC , BC .
 (1)、求抛物线的解析式;(2)、判断△ABC的形状,并说明理由;(3)、若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN , 将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为 , 点P的坐标为;(4)、抛物线对称轴上是否存在一点F , 使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.
(1)、求抛物线的解析式;(2)、判断△ABC的形状,并说明理由;(3)、若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN , 将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为 , 点P的坐标为;(4)、抛物线对称轴上是否存在一点F , 使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.