黑龙江省齐齐哈尔市甘南县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-29 类型:期末考试
一、单选题
-
1. 已知x=3是关于x的一元二次方程x2﹣2x﹣m=0的根,则该方程的另一个根是( )A、3 B、﹣3 C、1 D、﹣12. 下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 抛物线 经过平移得到抛物线 ,平移的方法是( )A、向左平移1个单位,再向下平移2个单位 B、向右平移1个单位,再向下平移2个单位 C、向左平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向上平移2个单位4. 若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形,则抽到的图形属于中心对称图形的概率是( )A、 B、 C、 D、5. 用min{a , b}表示a , b两数中的最小数,若函数 ,则y的图象为( )A、
3. 抛物线 经过平移得到抛物线 ,平移的方法是( )A、向左平移1个单位,再向下平移2个单位 B、向右平移1个单位,再向下平移2个单位 C、向左平移1个单位,再向上平移2个单位 D、向右平移1个单位,再向上平移2个单位4. 若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形,则抽到的图形属于中心对称图形的概率是( )A、 B、 C、 D、5. 用min{a , b}表示a , b两数中的最小数,若函数 ,则y的图象为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( )
6. 如图,在⊙O中,弦AB为8mm,圆心O到AB的距离为3mm,则⊙O的半径等于( ) A、3mm B、4mm C、5mm D、8mm7. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD=( )
A、3mm B、4mm C、5mm D、8mm7. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD=( ) A、128° B、100° C、64° D、32°8. 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
A、128° B、100° C、64° D、32°8. 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 二次函数y=a(x+k)2+k,无论k为何实数,其图象的顶点都在( )A、直线y=x上 B、直线y=﹣x上 C、x轴上 D、y轴上10. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为( )A、
A、 B、 C、 D、9. 二次函数y=a(x+k)2+k,无论k为何实数,其图象的顶点都在( )A、直线y=x上 B、直线y=﹣x上 C、x轴上 D、y轴上10. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为( )A、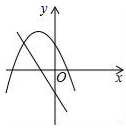 B、
B、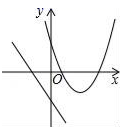 C、
C、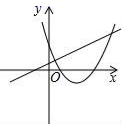 D、
D、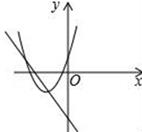
二、填空题
-
11. 点A(a,3)与点B(﹣4,b)关于原点对称,则a+b=.12. 设m , n分别为一元二次方程x2+2x-2 021=0的两个实数根,则m2+3m+n=.13. 若一个圆锥的底面圆半径为3cm,其侧面展开图的圆心角为120°,则圆锥的母线长是14. 若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .15. 如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1 cm,则BF=cm.
 16. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② >0;③ac-b+1=0;④OA·OB= .其中符合题意结论的个数是个.
16. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② >0;③ac-b+1=0;④OA·OB= .其中符合题意结论的个数是个. 17. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .
17. 如图,在平面直角坐标系中,将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线y= x上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y= x上,依次进行下去…,若点A的坐标是(0,1),点B的坐标是( ,1),则点A8的横坐标是 .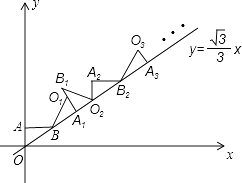
三、解答题
-
18. 解方程:(1)、x2+3=4x(2)、3x(x-3)=-419. 为进一步普及足球知识,传播足球文化,某市在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
 (1)、获得一等奖的学生有人;(2)、在本次知识竞赛活动中,A,B,C,D 四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.20. 如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B , 切点为D , ∠DAC=30°.
(1)、获得一等奖的学生有人;(2)、在本次知识竞赛活动中,A,B,C,D 四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.20. 如图,AD是⊙O的弦,AC是⊙O直径,⊙O的切线BD交AC的延长线于点B , 切点为D , ∠DAC=30°.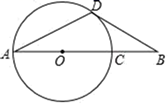 (1)、求证:△ADB是等腰三角形;(2)、若BC= ,求AD的长.21. 某超市欲购进一种今年新上市的产品,购进价为20元 件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量 件 与每件的销售价 元 件 之间有如下关系:(1)、请写出该超市销售这种产品每天的销售利润 元 与x之间的函数关系式,并求出超市能获取的最大利润是多少元.(2)、若超市想获取1500元的利润 求每件的销售价.(3)、若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?22. 在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ.
(1)、求证:△ADB是等腰三角形;(2)、若BC= ,求AD的长.21. 某超市欲购进一种今年新上市的产品,购进价为20元 件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量 件 与每件的销售价 元 件 之间有如下关系:(1)、请写出该超市销售这种产品每天的销售利润 元 与x之间的函数关系式,并求出超市能获取的最大利润是多少元.(2)、若超市想获取1500元的利润 求每件的销售价.(3)、若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?22. 在正方形 ABCD 中,M 是 BC 边上一点,且点 M 不与 B、C 重合,点 P 在射线 AM 上,将线段 AP 绕点 A 顺时针旋转 90°得到线段 AQ,连接BP,DQ. (1)、依题意补全图 1;(2)、①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;
(1)、依题意补全图 1;(2)、①连接 DP,若点 P,Q,D 恰好在同一条直线上,求证:DP2+DQ2=2AB2;②若点 P,Q,C 恰好在同一条直线上,则 BP 与 AB 的数量关系为: .
23. 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点. (1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为该抛物线的对称轴x=﹣1上的一个动点,直接写出使△BPC为直角三角形的点P的坐标.
(1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为该抛物线的对称轴x=﹣1上的一个动点,直接写出使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内有两点P(x1 , y1)、Q(x2 , y2),则线段PQ的长度PQ= ).