黑龙江省哈尔滨市香坊区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-29 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知抛物线的解析式为y=(x-2)2+1,则这条抛物线的顶点坐标是( ).A、(﹣2,1) B、(2,1) C、(2,﹣1) D、(1,2)3. 如图,⊙ 中, ,则 等于( )
2. 已知抛物线的解析式为y=(x-2)2+1,则这条抛物线的顶点坐标是( ).A、(﹣2,1) B、(2,1) C、(2,﹣1) D、(1,2)3. 如图,⊙ 中, ,则 等于( ) A、55° B、80° C、90° D、135°4. 已知反比例函数 的图象经过点 ,则这个函数的图象位于( )A、第二、三象限 B、第一、三象限 C、第三、四象限 D、第二、四象限5. 如图,滑雪场有一坡角α为20°的滑雪道,滑雪道AC的长为200米,则滑雪道的坡顶到坡底垂直高度AB的长为( )
A、55° B、80° C、90° D、135°4. 已知反比例函数 的图象经过点 ,则这个函数的图象位于( )A、第二、三象限 B、第一、三象限 C、第三、四象限 D、第二、四象限5. 如图,滑雪场有一坡角α为20°的滑雪道,滑雪道AC的长为200米,则滑雪道的坡顶到坡底垂直高度AB的长为( )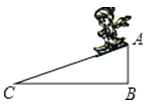 A、200tan20°米 B、米 C、200sin20°米 D、200cos20°米6. 将抛物线 向左平移3个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为( )A、 B、 C、 D、7. 某水果园2017年水果产量为50吨,2019年水果产量为70吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为 ,则根据题意可列方程为( )A、 B、 C、 D、8. 如图, 中, ,将 绕着点 旋转至 ,点 的对应点点 恰好落在 边上.若 , ,则 的长为( )
A、200tan20°米 B、米 C、200sin20°米 D、200cos20°米6. 将抛物线 向左平移3个单位长度,再向上平移3个单位长度后,所得抛物线的解析式为( )A、 B、 C、 D、7. 某水果园2017年水果产量为50吨,2019年水果产量为70吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为 ,则根据题意可列方程为( )A、 B、 C、 D、8. 如图, 中, ,将 绕着点 旋转至 ,点 的对应点点 恰好落在 边上.若 , ,则 的长为( ) A、2 B、3 C、 D、49. 如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是( )
A、2 B、3 C、 D、49. 如图,点D是△ABC的边AB上的一点,过点D作BC的平行线交AC于点E,连接BE,过点D作BE的平行线交AC于点F,则下列结论错误的是( ) A、 B、 C、 D、10. 已知二次函数 的图象如图所示,下列结论:① ,② ,③ ,④ ,其中符合题意结论的个数为( )
A、 B、 C、 D、10. 已知二次函数 的图象如图所示,下列结论:① ,② ,③ ,④ ,其中符合题意结论的个数为( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 函数 中,自变量 的取值范围是.12. 计算 .13. 在平面直角坐标系中,点(﹣2,3)关于原点对称的点的坐标是 .14. 若正六边形的边长为2,则此正六边形的边心距为 .15. 如图, 是半圆 的直径,四边形 内接于圆 ,连接 , ,则 度.
 16. 如图,□ 中, , , 的周长为25,则 的周长为 .
16. 如图,□ 中, , , 的周长为25,则 的周长为 . 17. 若弧长为4π的扇形的圆心角为直角,则该扇形的半径为 .18. 已知:等边△ABC,点P是直线BC上一点,且PC:BC=1:4,则tan∠APB= ,19. 如图,双曲线 经过 斜边 的中点 ,与直角边 交于点 .过点 作 于点 ,连接 ,则 的面积是 .
17. 若弧长为4π的扇形的圆心角为直角,则该扇形的半径为 .18. 已知:等边△ABC,点P是直线BC上一点,且PC:BC=1:4,则tan∠APB= ,19. 如图,双曲线 经过 斜边 的中点 ,与直角边 交于点 .过点 作 于点 ,连接 ,则 的面积是 .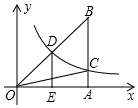 20. 如图,四边形 中, ,连接 , ,点 为 中点,连接 , , ,则 .
20. 如图,四边形 中, ,连接 , ,点 为 中点,连接 , , ,则 .
三、解答题
-
21. 化简求值: ,其中a=2cos30°+tan45°.22. 图中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.线段 和 的端点 均在格点上.
 (1)、在图中画出以 为一边的 ,点 在格点上,使 的面积为4,且 的一个角的正切值是 ;(2)、在图中画出以 为顶角的等腰 (非直角三角形),点 在格点上.请你直接写出 的面积.23. 如图,在平面直角坐标系中,直线AB与x轴交于点B , 与y轴交于点A , 直线AB与反比例函数y= (m>0)在第一象限的图象交于点C、点D , 其中点C的坐标为(1,8),点D的坐标为(4,n).
(1)、在图中画出以 为一边的 ,点 在格点上,使 的面积为4,且 的一个角的正切值是 ;(2)、在图中画出以 为顶角的等腰 (非直角三角形),点 在格点上.请你直接写出 的面积.23. 如图,在平面直角坐标系中,直线AB与x轴交于点B , 与y轴交于点A , 直线AB与反比例函数y= (m>0)在第一象限的图象交于点C、点D , 其中点C的坐标为(1,8),点D的坐标为(4,n). (1)、分别求m、n的值;(2)、连接OD , 求△ADO的面积.24. 已知,正方形 中,点 是边 延长线上一点,连接 ,过点 作 ,垂足为点 , 与 交于点 .
(1)、分别求m、n的值;(2)、连接OD , 求△ADO的面积.24. 已知,正方形 中,点 是边 延长线上一点,连接 ,过点 作 ,垂足为点 , 与 交于点 . (1)、如图甲,求证: ;(2)、如图乙,连接 ,若 , ,求 的值.25. 某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映:每涨价1元,每星期要少卖出10件.(1)、每件商品涨价多少元时,每星期该商品的利润是4000元?(2)、每件商品的售价为多少元时,才能使每星期该商品的利润最大?最大利润是多少元?26. 已知: 内接于⊙ ,连接 并延长交 于点 ,交⊙ 于点 ,满足 .
(1)、如图甲,求证: ;(2)、如图乙,连接 ,若 , ,求 的值.25. 某商品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查反映:每涨价1元,每星期要少卖出10件.(1)、每件商品涨价多少元时,每星期该商品的利润是4000元?(2)、每件商品的售价为多少元时,才能使每星期该商品的利润最大?最大利润是多少元?26. 已知: 内接于⊙ ,连接 并延长交 于点 ,交⊙ 于点 ,满足 . (1)、如图1,求证: ;(2)、如图2,连接 ,点 为弧 上一点,连接 , = ,过点 作 ,垂足为点 ,求证: ;(3)、如图3,在(2)的条件下,点 为 上一点,分别连接 , ,过点 作 ,交⊙ 于点 , , ,连接 ,求 的长.27. 已知,在平面直角坐标系中,二次函数 的图象与 轴交于点 ,与 轴交于点 ,点 的坐标为 ,点 的坐标为 .
(1)、如图1,求证: ;(2)、如图2,连接 ,点 为弧 上一点,连接 , = ,过点 作 ,垂足为点 ,求证: ;(3)、如图3,在(2)的条件下,点 为 上一点,分别连接 , ,过点 作 ,交⊙ 于点 , , ,连接 ,求 的长.27. 已知,在平面直角坐标系中,二次函数 的图象与 轴交于点 ,与 轴交于点 ,点 的坐标为 ,点 的坐标为 . (1)、如图1,分别求 的值;(2)、如图2,点 为第一象限的抛物线上一点,连接 并延长交抛物线于点 , ,求点 的坐标;(3)、在(2)的条件下,点 为第一象限的抛物线上一点,过点 作 轴于点 ,连接 、 ,点 为第二象限的抛物线上一点,且点 与点 关于抛物线的对称轴对称,连接 ,设 , ,点 为线段 上一点,点 为第三象限的抛物线上一点,分别连接 ,满足 , ,过点 作 的平行线,交 轴于点 ,求直线 的解析式.
(1)、如图1,分别求 的值;(2)、如图2,点 为第一象限的抛物线上一点,连接 并延长交抛物线于点 , ,求点 的坐标;(3)、在(2)的条件下,点 为第一象限的抛物线上一点,过点 作 轴于点 ,连接 、 ,点 为第二象限的抛物线上一点,且点 与点 关于抛物线的对称轴对称,连接 ,设 , ,点 为线段 上一点,点 为第三象限的抛物线上一点,分别连接 ,满足 , ,过点 作 的平行线,交 轴于点 ,求直线 的解析式.