黑龙江省哈尔滨市平房区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-29 类型:期末考试
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 下列运算中,结果正确的是( )A、 B、 C、 D、3. 下列图形中是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 若反比例函数 的图像经过点 ,则下列各点在该函数图象上的为( )A、 B、 C、 D、5. 下面是由几个小正方体搭成的几何体,则这个几何体的左视图为( )
4. 若反比例函数 的图像经过点 ,则下列各点在该函数图象上的为( )A、 B、 C、 D、5. 下面是由几个小正方体搭成的几何体,则这个几何体的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 在 中, , ,若 ,则 的长为( ).A、 B、 C、 D、7. 如图, 为圆 的切线, 交圆 于点 , 为圆 上一点,若 ,则 的度数为( ).
6. 在 中, , ,若 ,则 的长为( ).A、 B、 C、 D、7. 如图, 为圆 的切线, 交圆 于点 , 为圆 上一点,若 ,则 的度数为( ). A、 B、 C、 D、8. 二次函数 经过平移后得到二次函数 ,则平移方法可为( )A、向左平移1个单位,向上平移1个单位 B、向左平移1个单位,向下平移1个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移1个单位,向上平移1个单位9. 如图,将一边长AB为4的矩形纸片折叠,使点D与点B重合,折痕为EF , 若EF=2 ,则矩形的面积为( )
A、 B、 C、 D、8. 二次函数 经过平移后得到二次函数 ,则平移方法可为( )A、向左平移1个单位,向上平移1个单位 B、向左平移1个单位,向下平移1个单位 C、向右平移1个单位,向下平移1个单位 D、向右平移1个单位,向上平移1个单位9. 如图,将一边长AB为4的矩形纸片折叠,使点D与点B重合,折痕为EF , 若EF=2 ,则矩形的面积为( )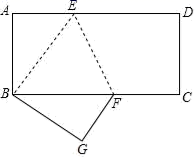 A、32 B、28 C、30 D、3610. 四边形 为平行四边形,点 在 的延长线上,连接 交 于点 ,则下列结论正确的是( )
A、32 B、28 C、30 D、3610. 四边形 为平行四边形,点 在 的延长线上,连接 交 于点 ,则下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将数12500000用科学记数法表示为 .12. 计算 的结果是.13. 在函数 中,自变量x的取值范围是 .14. 把多项式 分解因式的结果是 .15. 不等式组 的解集为 .16. 已知扇形的弧长为4π,圆心角为120°,则它的半径为 .17. 分式方程 = 的解是 .18. 一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,张兵同学掷一次骰子,骰子向上的一面出现的点数是3的倍数的概率是 .19. 已知 中, , , ,则 的长为 .20. 如图, 为等边三角形,点 在 外,连接 、 .若 , , ,则 .

三、解答题
-
21. 先化简,再求代数式 的值,其中22. 如图为正方形网格,每个小正方形的边长均为1,各个小正方形的顶点叫做格点,请在下面的网格中按要求分别画图,使得每个图形的顶点均在格点上.
 (1)、在图中画一个以 为一边的菱形 ,且菱形 的面积等于20.(2)、在图中画一个以 为对角线的正方形 ,并直接写出正方形 的面积.23. 哈尔滨市教育局以冰雪节为契机,在全市校园内开展多姿多彩的冰雪活动.某校为激发学生参与冰雪体育活动热情,开设了“滑冰、抽冰尜、冰球、冰壶、雪地足球”五个冰雪项目,并开展了以“我最喜欢的冰雪项目”为主题的调查活动,围绕“在滑冰、抽冰尜、冰球、冰壶、雪地足球中,你最喜欢的冰雪项目是什么?(每名学生必选且只选一个)”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整的统计图.请根据统计图的信息回答下列问题:
(1)、在图中画一个以 为一边的菱形 ,且菱形 的面积等于20.(2)、在图中画一个以 为对角线的正方形 ,并直接写出正方形 的面积.23. 哈尔滨市教育局以冰雪节为契机,在全市校园内开展多姿多彩的冰雪活动.某校为激发学生参与冰雪体育活动热情,开设了“滑冰、抽冰尜、冰球、冰壶、雪地足球”五个冰雪项目,并开展了以“我最喜欢的冰雪项目”为主题的调查活动,围绕“在滑冰、抽冰尜、冰球、冰壶、雪地足球中,你最喜欢的冰雪项目是什么?(每名学生必选且只选一个)”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整的统计图.请根据统计图的信息回答下列问题: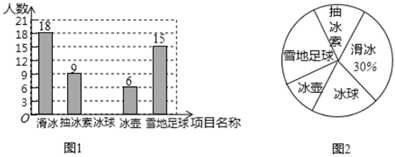 (1)、本次调查共抽取了多少名学生?(2)、求本次调查中,最喜欢冰球项目的人数,并补全条形统计图;(3)、若该中学共有1800名学生,请你估计该中学最喜欢雪地足球的学生约有多少名.24. 如图1, 中, , 是 的中点, 平分 交 于点 , 在 的延长线上且 .
(1)、本次调查共抽取了多少名学生?(2)、求本次调查中,最喜欢冰球项目的人数,并补全条形统计图;(3)、若该中学共有1800名学生,请你估计该中学最喜欢雪地足球的学生约有多少名.24. 如图1, 中, , 是 的中点, 平分 交 于点 , 在 的延长线上且 . (1)、求证:四边形 是平行四边形;(2)、如图2若四边形 是菱形,连接 , , 与 交于点 ,连接 ,在不添加任何辅助线的情况下,请直接写出图2中的所有等边三角形.25. 某校为了普及推广冰雪活动进校园,准备购进速滑冰鞋和花滑冰鞋用于开展冰上运动,若购进30双速滑冰鞋和20双花滑冰鞋共需8500元;若购进40双速滑冰鞋和10双花滑冰鞋共需8000元.(1)、求速滑冰鞋和花滑冰鞋每双购进价格分别为多少元?(2)、若该校购进花滑冰鞋的数量比购进速滑冰鞋数量的2倍少10双,且用于购置两种冰鞋的总经费不超过9000元,则该校至多购进速滑冰鞋多少双?26. 已知: 、 是圆 中的两条弦,连接 交 于点 ,点 在 上,连接 , .
(1)、求证:四边形 是平行四边形;(2)、如图2若四边形 是菱形,连接 , , 与 交于点 ,连接 ,在不添加任何辅助线的情况下,请直接写出图2中的所有等边三角形.25. 某校为了普及推广冰雪活动进校园,准备购进速滑冰鞋和花滑冰鞋用于开展冰上运动,若购进30双速滑冰鞋和20双花滑冰鞋共需8500元;若购进40双速滑冰鞋和10双花滑冰鞋共需8000元.(1)、求速滑冰鞋和花滑冰鞋每双购进价格分别为多少元?(2)、若该校购进花滑冰鞋的数量比购进速滑冰鞋数量的2倍少10双,且用于购置两种冰鞋的总经费不超过9000元,则该校至多购进速滑冰鞋多少双?26. 已知: 、 是圆 中的两条弦,连接 交 于点 ,点 在 上,连接 , . (1)、如图1,若 ,求证:弧 弧 ;(2)、如图2,连接 ,若 ,求证: ;(3)、如图3,在第(2)问的条件下,延长 交圆 于点 ,点 在 上,连接 ,若 , , ,求线段 的长.27. 在平面直角坐标系 中,直线 交 轴于点 ,交 轴于点 , ,点 的坐标是 .
(1)、如图1,若 ,求证:弧 弧 ;(2)、如图2,连接 ,若 ,求证: ;(3)、如图3,在第(2)问的条件下,延长 交圆 于点 ,点 在 上,连接 ,若 , , ,求线段 的长.27. 在平面直角坐标系 中,直线 交 轴于点 ,交 轴于点 , ,点 的坐标是 . (1)、如图1,求直线 的解析式;(2)、如图2,点 在第一象限内,连接 ,过点 作 交 延长线于点 ,且 ,过点 作 轴于点 ,连接 ,设点 的横坐标为 , 的面积为S,求S与 的函数关系式(不要求写出自变量 的取值范围);(3)、如图3,在(2)的条件下,过点 作 轴,连接 、 ,若 , 时,求 的值.
(1)、如图1,求直线 的解析式;(2)、如图2,点 在第一象限内,连接 ,过点 作 交 延长线于点 ,且 ,过点 作 轴于点 ,连接 ,设点 的横坐标为 , 的面积为S,求S与 的函数关系式(不要求写出自变量 的取值范围);(3)、如图3,在(2)的条件下,过点 作 轴,连接 、 ,若 , 时,求 的值.