黑龙江省哈尔滨市道里区2019-2020学年九年级上学期数学期末试卷
试卷更新日期：2020-10-29 类型：期末考试
一、单选题
-
1. 下列中式元素的图案中，既是中心对称图形又是轴对称图形的是（ ）A、
B、
C、
D、
2. 五个完全相同的正方体搭成的几何体如图所示，其主视图是（ ）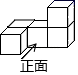
A、
B、
C、
D、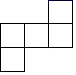
3. 将抛物线y＝x2﹣2向右平移3个单位长度，再向上平移2个单位长度，则所得抛物线的解析式为（ ）A、y＝（x+3）2 B、y＝（x﹣3）2 C、y＝（x+2）2+1 D、y＝（x﹣2）2+14. 在△ABC中，∠C＝90°，sinA＝ ，则tanB等于（ ）A、 B、 C、 D、5. 已知点P1（a，2）与点P2（﹣3，b）关于原点对称，则a﹣b的值是（ ）A、﹣5 B、﹣1 C、1 D、56. 在反比例函数y＝ 图象的每一条曲线上，y都随x的增大而增大，则k的取值范围是（ ）A、k＞2 B、k＞0 C、k≥2 D、k＜27. 随机掷一枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，则这个骰子向上的一面点数大于3的概率为 （ ）A、 B、 C、 D、8. 关于抛物线y＝﹣（x+3）2+2，下列说法错误的是（ ）A、开口向下 B、对称轴是直线x＝﹣3 C、与y轴交点坐标（0，2） D、顶点坐标（﹣3，2）9. 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为（ ）
A、100° B、110° C、115° D、120°10. 如图，平行四边形ABCD中，连接AC ， 在CD的延长线上取一点E ， 连接BE ， 分别交AC和AD于点G和点F ， 则下列结论错误的是（ ）
A、 ＝ B、 ＝ C、 ＝ D、 ＝二、填空题
-
11. 函数 中，自变量 的取值范围是12. 若二次函数y＝x2﹣6x+3a的图象与x轴有且只有一个交点，则a的值为 ．13. 身高1.5米的小强站在旗杆旁，测得小强和旗杆在地面上的影长分别为2米和16米，则旗杆的高度为米．14. 一个扇形的半径为6，弧长为3π，则此扇形的圆心角为度．15. 汽车刹车后行驶的距离s与行驶时间t（秒）的函数关系是s＝15t﹣6t2 ， 汽车从刹车到停下来所用时间是秒.16. 如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D，若OD=2，tan∠OAB= ，则AB的长是 ．
17. 科技改变生活，手机导航极大方便了人们的出行．如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西60°方向行驶6千米至B地，再沿北偏东45°方向行驶一段距离到达古镇C ． 小明发现古镇C恰好在A地的正北方向，则B、C两地的距离是千米．
18. 如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，将△ABC绕点A逆时针旋转得到△AB′C′，点B、C的对应点分别为点B'、C′，AB′与BC相交于点D ， 当B′C′∥AB时，则CD＝ ．
19. 如图，CD是⊙O的直径，AB是⊙O的弦，CD⊥AB ， 垂足为E ， 连接BC、BD ． 点F为线段CB上一点，连接DF ， 若CE＝2，AB＝8，BF＝ ，则tan∠CDF＝ ．
20. 如图，P是等边三角形ABC内一点，连接PA、PC ， PA＝PC ， ∠APC＝90°，把线段AP绕点A逆时针旋转120°，得到线段AQ（点P与点Q为对应点），连接BQ交AP于点E ． 点D为BQ的中点，连接AD、PD ， 若S△DAP＝2，则AB＝ ．
三、解答题
-
21. 先化简，再求代数式（1﹣ ）÷ 的值，其中x＝2sin60°﹣tan45°．22. 如图，在每个小正方形的边长均为1的方格纸中，线段AB的端点均在小正方形的顶点上．
(1)、在图中画出以AB为底的等腰三角形ABC ， 点C在小正方形的顶点上，且△ABC的面积是7.5；(2)、在（1）的条件下，在图中画出以AC为斜边的直角三角形ACE（AE＜EC），点E在小正方形的顶点上，且△ACE的面积是5，连接EB ， 并直接写出tan∠AEB的值．23. 某中学在艺术节期间向全校学生征集书画作品，美术王老师从全校随机抽取了四个班级记作A、B、C、D，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图.
(1)、王老师抽查的四个班级共征集到作品多少件？(2)、请把图2的条形统计图补充完整；(3)、若全校参展作品中有五名同学获得一等奖，其中有三名男生、二名女生.现在要在其中抽两名同学去参加学校总结表彰座谈会，请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率.24. 在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，将△ABC绕点A顺时针旋转60°，得到△AED ， 点B、C的对应点分别是E、D ． F为AC的中点，连接BF、DF、BE ， DF与EA相交于点G ， BE与AC相交于点H ．
(1)、如图1，求证：四边形BFDE为平行四边形；(2)、如图2，连接CE ， 在不添加任何辅助线与字母的情况下，请直接写出所有与△AEC全等的三角形．25. 某超市有甲、乙两种商品，若买1件甲商品和2件乙商品，共需80元；若买2件甲商品和3件乙商品，共需135元．(1)、求甲、乙两种商品每件售价分别是多少元；(2)、甲商品每件的成本是20元，根据市场调查：若按（1）中求出的单价销售，该超市每天销售甲商品100件；若销售单价每上涨1元，甲商品每天的销售量就减少5件．写出甲商品每天的销售利润y（元）与销售单价（x）元之间的函数关系，并求每件售价为多少元时，甲商品每天的销售利润最大，最大利润是多少？26. 已知：△ABC是⊙O的内接三角形，AB为直径，AC＝BC ， D、E是⊙O上两点，连接AD、DE、AE ．
(1)、如图1，求证：∠AED﹣∠CAD＝45°；(2)、如图2，若DE⊥AB于点H ， 过点D作DG⊥AC于点G ， 过点E作EK⊥AD于点K ， 交AC于点F ， 求证：AF＝2DG；(3)、如图3，在（2）的条件下，连接DF、CD ， 若∠CDF＝∠GAD ， DK＝3，求⊙O的半径．27. 在平面直角坐标系中，点O为坐标原点，抛物线y＝ ax2+ ax+ a（a≠0）交x轴于点A和点B（点A在点B左边），交y轴于点C ， 连接AC ， tan∠CAO＝3．
(1)、如图1，求抛物线的解析式；(2)、如图2，D是第一象限的抛物线上一点，连接DB ， 将线段DB绕点D顺时针旋转90°，得到线段DE（点B与点E为对应点），点E恰好落在y轴上，求点D的坐标；(3)、如图3，在（2）的条件下，过点D作x轴的垂线，垂足为H ， 点F在第二象限的抛物线上，连接DF交y轴于点G ， 连接GH ， sin∠DGH＝ ，以DF为边作正方形DFMN ， P为FM上一点，连接PN ， 将△MPN沿PN翻折得到△TPN（点M与点T为对应点），连接DT并延长与NP的延长线交于点K ， 连接FK ， 若FK＝ ，求cos∠KDN的值．