黑龙江齐齐哈尔市建华区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-10-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列银行标志图片中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如果x=4是一元二次方程x²－3x=a²的一个根，则常数a的值是（）

A、2 B、﹣2 C、±2 D、±4

查看试题解析
3. 一人乘雪橇沿如图所示的斜坡（倾斜角为30°）笔直滑下，滑下的距离为24米，则此人下滑的高度为（）

A、24 B、 $12 \sqrt{3}$ C、12 D、6

查看试题解析
4. 如图，将 $Δ A B C$ 绕点 $A$ 顺时针旋转，得到 $Δ A D E$ ，且点 $D$ 在 $A C$ 上，下列说法错误的是（）

A、 $A C$ 平分 $∠ B A E$ B、 $A B = A D$ C、 $B C / / A E$ D、 $B C = D E$

查看试题解析
5. 函数 $y = \frac{k}{x} (k \neq 0)$ 的图象如图所示，那么函数 $y = k x - k$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在⊙O中，若点C是 $\overset{⌢}{A B}$ 的中点，∠A=50°，则∠BOC=（）

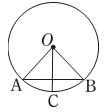A、40° B、45° C、50° D、60°

查看试题解析
7. 某厂今年3月的产值为50万元，5月份上升到72万元，这两个月平均每月增长的百分率是多少？若设平均每月增长的百分率为x，则列出的方程正确的是（）

A、50（1+x）=72 B、50（1+x）＋50（1+x）²=72 C、50（1+x）×2=72 D、50（1+x）²=72

查看试题解析
8. 一个几何体由若干个相同的正方体组成，其主视图和左视图如图所示，则组成这个几何体的正方体个数最小值为（）

A、5 B、6 C、7 D、8

查看试题解析
9. 如图，在平行四边形 $A B C D$ 中， $A B ： A D = 3 ： 2$ ， $∠ A D B = 60 °$ ，那么 $\sin A$ 的值等于（）

A、 $\frac{3 - \sqrt{6}}{6}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3} + 2 \sqrt{2}}{6}$ D、 $\frac{\sqrt{3} + 3 \sqrt{2}}{6}$

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图象如图，则下列说法：① $c = 0$ ；②该抛物线的对称轴是直线 $x = - 1$ ；③当 $x = 1$ 时， $y = 2 a$ ；④当 $m < - 2$ 时， $a m^{2} + b m > 0$ ；其中正确的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 当m时，关于 $x$ 的方程 $(m^{2} - 1) x^{2} + 2 (m - 1) x + 1 = 0$ 有实数根．

查看试题解析
12. 某商场在“元旦”期间推出购物摸奖活动，摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个.顾客摸奖时，一次摸出两个球，如果两个球的颜色相同就得奖，颜色不同则不得奖.那么顾客摸奖一次，得奖的概率是．

查看试题解析
13. 如图，半径为3的圆 $A$ 经过原点 $O$ 和点 $B （ 0 ， 2 ）$ ，点 $C$ 是 $y$ 轴左侧圆 $A$ 优弧上一点，则 $\tan ∠ O C B =$ ．

查看试题解析
14. 在Rt△ABC中，斜边AB=4，∠B=60°，将△ABC绕点B旋转60°，顶点C运动的路线长是（结果保留π）．

查看试题解析
15. 半径为 $\sqrt{2}$ 的圆 $O$ 中，弦 $A B$ 、 $A C$ 的长分别为2和 $\sqrt{6}$ ，则 $∠ B A C$ 的度数为．

查看试题解析
16. 如图，矩形 $A B C D$ 的对角线 $B D$ 经过坐标原点，矩形的边分别平行于坐标轴，点 $A$ 在反比例函数 $y = \frac{a^{2} + 2 a + 1}{x}$ 的图象上.若点 $C$ 的坐标为 $(- 2 ， - 2)$ ，则 $a$ 的值为．

查看试题解析
17. 在平面直角坐标系中，解析式为 $y = \sqrt{3} x + 1$ 的直线 $a$ 、解析式为 $y = \frac{\sqrt{3}}{3} x$ 的直线 $b$ 如图所示，直线 $a$ 交 $y$ 轴于点 $A$ ，以 $O A$ 为边作第一个等边三角形 $Δ O A B$ ，过点 $B$ 作 $y$ 轴的平行线交直线 $a$ 于点 $A_{1}$ ，以 $A_{1} B$ 为边作第二个等边三角形 $Δ A_{1} B B_{1}$ ，……顺次这样做下去，第2020个等边三角形的边长为．

查看试题解析

三、解答题

18.

(1)、解方程 $x^{2} + 9 x - 8 = 0$ ．

(2)、计算： $- 2^{2} + \sqrt{8} \sin 45^{\circ} - 2^{- 1} + {(3.14 - π)}^{0}$ ．

查看试题解析
19. 直线 $y = k_{1} x + b$ 与双曲线 $y = \frac{k_{2}}{x}$ 只有一个交点 $A （ 1 ， 2 ）$ ，且与 $x$ 轴、 $y$ 轴分别交于 $B$ 、 $C$ 两点，AD垂直平分 $O B$ ，交 $x$ 轴于点 $D$ ．

(1)、求直线 $y = k_{1} x + b$ 、双曲线 $y = \frac{k_{2}}{x}$ 的解析式；

(2)、过点 $B$ 作 $x$ 轴的垂线交双曲线 $y = \frac{k_{2}}{x}$ 于点 $E$ ，求 $Δ A B E$ 的面积．

查看试题解析
20. 如图，某中学有一块长为 $a$ 米，宽为 $b$ 米的矩形场地，计划在该场地上修筑宽都为2米的两条互相垂直的道路（阴影部分），余下的四块矩形小场地建成草坪．

(1)、请分别写出每条道路的面积（用含 $a$ 或 $b$ 的代数式表示）；

(2)、若 $a ： b = 2 ： 1$ ，并且四块草坪的面积之和为144平方米，试求原来矩形场地的长与宽各为多少米？

查看试题解析
21. 如图，在 $Δ A B C$ 中，点 $D$ 在 $B C$ 边上，点 $E$ 在 $A C$ 边上，且 $A D = A B$ ， $∠ D E C = ∠ A D B$ ．

(1)、求证： $Δ A E D$ ∽ $Δ A D C$ ；

(2)、若 $A E = 1$ ， $E C = 3$ ，求 $A B$ 的长．

查看试题解析
22. 甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示．游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．

(1)、用列表法（或画树状图）求甲获胜的概率；

(2)、你认为这个游戏规则对双方公平吗？请简要说明理由．

查看试题解析
23. 如图， $A B$ 是圆 $O$ 的直径， $A E$ 平分 $∠ B A F$ ，交圆 $O$ 于点 $E$ ，过点 $E$ 作直线 $E D ⊥ A F$ ，交 $A F$ 的延长线于点 $D$ ，交 $A B$ 的延长线于点 $C$ ．

(1)、求证： $C D$ 是圆 $O$ 的切线；

(2)、若 $C B = 2$ ， $C E = 4$ ，求 $A E$ 的长．

查看试题解析
24. 如图，平面直角坐标系中，点 $A$ 、点 $B$ 在 $x$ 轴上（点 $A$ 在点 $B$ 的左侧），点 $C$ 在第一象限，满足 $∠ A C B$ 为直角，且恰使 $Δ O C A$ ∽△ $Δ O B C$ ，抛物线 $y = a x^{2} - 8 a x + 12 a (a < 0)$ 经过 $A$ 、 $B$ 、 $C$ 三点．

(1)、求线段 $O B$ 、 $O C$ 的长；

(2)、求点 $C$ 的坐标及该抛物线的函数关系式；

(3)、在 $x$ 轴上是否存在点 $P$ ，使 $Δ B C P$ 为等腰三角形？若存在，求出所有符合条件的 $P$ 点的坐标，若不存在，请说明理由．

查看试题解析