黑龙江省齐齐哈尔市铁锋区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段能组成三角形的是（）

A、 $2, 3, 5$ B、 $7, 4, 2$ C、 $3, 4, 8$ D、 $3, 3, 4$

查看试题解析
2. 在下列“禁毒”、“和平”、“志愿者”、“节水”这四个标志中，属于轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 ${(- 1)}^{- 1} = 1$ B、 ${(x + 2)}^{2} = x^{2} + 4$ C、 ${(a b^{3})}^{2} = a^{2} b^{5}$ D、 $4 a^{3} b \div (- 2 a^{2} b) = - 2 a$

查看试题解析
4. 下面式子从左边到右边的变形中是因式分解的是（）

A、 $x^{2} - x - 2 = x (x - 1) - 2$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 $x^{2} - 4 = (x + 2) (x - 2)$ D、 $x - 1 = x (1 - \frac{1}{x})$

查看试题解析
5. 如图，在 $Δ A B C$ 中，高 $B D ， C F$ 相交于点 $E$ ，若 $∠ A = 52^{°}$ ，则 $∠ B E C =$ （）

A、 $116^{°}$ B、 $128^{°}$ C、 $138^{°}$ D、 $142^{°}$

查看试题解析
6. 如图，已知E，B，F，C四点在一条直线上， $EB = CF$ ， $∠ A = ∠ D$ ，添加以下条件之一，仍不能证明 $△ ABC$ ≌ $△ DEF$ 的是 $($ $)$

A、 $∠ E = ∠ ABC$ B、 $AB = DE$ C、 $AB / / DE$ D、 $DF / / AC$

查看试题解析
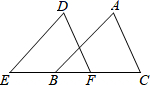7. 如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，且∠ADC=110°，则∠MAB=（）

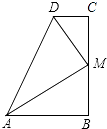A、30° B、35° C、45° D、60°

查看试题解析
8. 如果把分式 $\frac{x + y}{x y}$ 中的x、y同时扩大为原来的2倍，那么该分式的值（　　）

A、不变 B、扩大为原来的2倍 C、缩小为原来的 $\frac{1}{2}$ D、缩小为原来的 $\frac{1}{4}$

查看试题解析
9. 若关于x的分式方程 $\frac{x - a}{x + 1} = a$ 无解，则a的值为（）

A、1 B、-1 C、1或0 D、1或-1

查看试题解析
10. 如图，把一张长方形纸片 $A B C D$ 沿对角线 $B D$ 折叠，点 $C$ 的对应点为 $E$ ， $B E$ 与 $A D$ 相交于点 $F$ ，则下列结论不一定成立的是（）

A、 $Δ B F D$ 是等腰三角形 B、 $Δ A B F ≅ Δ E D F$ C、 $B E$ 平分 $∠ A B D$ D、折叠后的图形是轴对称图形

查看试题解析

二、填空题

11. 在人体血液中，红细胞直径约为 $0.00077 c m$ ，数据0.00077用科学记数法表示为．

查看试题解析
12. 若n边形的内角和是它的外角和的2倍，则n=.

查看试题解析
13. 若关于x的二次三项式 $x^{2} + (m - 1) x + 16$ 是完全平方式，则m的值为．

查看试题解析
14. 如图， $∠ A B C = 50^{°}$ ， $B D$ 平分 $∠ A B C$ ，过 $D$ 作 $D E / / A B$ 交于 $B C$ 于点 $E$ ，若点 $F$ 在射线 $B A$ 上，且满足 $D F = D E$ ，则 $∠ D F B$ 的度数为．

查看试题解析
15. 如图，等腰三角形ABC的底边BC长为6，面积是18，腰AC的垂直平分线EF分别交AC ， AB于E ， F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM的周长的最小值为．

查看试题解析
16. 如图，在平面直角坐标系中，点 $A_{1} ， A_{2} ， A_{3} ...$ 都在 $x$ 轴上，点 $B_{1} ， B_{2} ， B_{3} ...$ 都在第一象限的角平分线上， $Δ B_{1} A_{1} A_{2} ， Δ B_{2} A_{2} A_{3} ， Δ B_{3} A_{3} A_{4} ...$ 都是等腰直角三角形，且 $O A_{1} = 1$ ，则点 $B_{2020}$ 的坐标为．

查看试题解析

三、解答题

17. 计算与化简求值：

(1)、 ${(\frac{2}{3})}^{- 2} - {(π - 3.14)}^{0} + {(\frac{1}{2})}^{2020} \times {(- 2)}^{2020}$

(2)、 $(x + 2 y) (x - y) - {(x - y)}^{2}$

(3)、化简 $\frac{a}{a + 1} \div (a - 1 - \frac{2 a - 1}{a + 1})$ ，并选一个合适的数作为 $a$ 的值代入求值．

查看试题解析
18. 因式分解：

(1)、 $8 a x^{2} - 2 a$

(2)、 $4 a^{2} - 3 b (4 a - 3 b)$

查看试题解析
19. 解方程： $\frac{8}{x^{2} - 4}$ +1＝ $\frac{x}{x - 2}$ .

查看试题解析
20. 如图，在 $Δ A B C$ 中， $A D$ 是 $B C$ 边上的高， $A E$ 是 $Δ A B C$ 的角平分线， $B E = A E ， ∠ B = 40^{°}$ ．

(1)、求 $∠ E A D$ 的度数；

(2)、若 $C D = 1$ ，求 $A C$ 的长．

查看试题解析
21. 如图①，一个长为 $2 a$ ，宽为 $2 b$ 的长方形，沿途中的虚线用剪刀均匀的分成四个小长方形，然后按图②的形状拼成一个正方形．

(1)、观察图②，请用两种不同的方法求图②中阴影部分的面积．
方法1：（只列式，不化简）

方法2：（只列式，不化简）

(2)、请写出 ${(a - b)}^{2} ， {(a + b)}^{2} ， a b$ 三个式子之间的等量关系：．

(3)、根据（2）题中的等量关系，解决如下问题：若 $a + b = 2 ， a b = \frac{3}{4}$ ，求a-b的值．

查看试题解析
22. 去年冬天某市遭遇持续暴雪天气，该市启用了清雪机，已知一台清雪机的工作效率相当于一名环卫工人工作效率的200倍，若用这台清雪机清理6000立方米的雪，要比120名环卫工人清理这些雪少用 $\frac{8}{3}$ 小时，试求一台清雪机每小时清雪多少立方米．

查看试题解析
23. 综合与实践

(1)、问题发现
如图1， $Δ A C B$ 和 $Δ D C E$ 均为等边三角形，点 $A ， D ， E$ 在同一直线上，连接 $B E$ ．请写出 $∠ A E B$ 的度数及线段 $A D ， B E$ 之间的数量关系，并说明理由．

(2)、类比探究
如图2， $Δ A C B$ 和 $Δ D C E$ 均为等腰直角三角形， $∠ A C B = ∠ D C E = 90^{°}$ ，点 $A ， D ， E$ 在同一直线上， $C M$ 为 $Δ D C E$ 中 $D E$ 边上的高，连接 $B E$ ．

填空：① $∠ A E B$ 的度数为；

②线段 $C M ， A E ， B E$ 之间的数量关系为．

(3)、拓展延伸
在（2）的条件下，若 $B E = 4 ， C M = 3$ ，则四边形 $A B E C$ 的面积为．

查看试题解析