黑龙江省牡丹江市2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列国旗中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 ${(- x)}^{2} \cdot {(- x)}^{3} = - x^{6}$ B、 ${[{(x - y)}^{2}]}^{m + 2} = {(x - y)}^{2 m + 4}$ C、 ${(- 3 a^{3} b^{2} c)}^{4} = - 81 a^{12} b^{8} c^{4}$ D、 $a^{3} \div a^{3} = 0$

查看试题解析
3. 下列等式从左到右的变形，错误的是（）

A、 $\frac{x^{4}}{x^{3} - 2 x^{2}} = \frac{x^{2}}{x - 2}$ B、 $\frac{x - y}{x^{2} - y^{2}} = \frac{1}{x + y}$ C、 $\frac{0.03 x - 0.2 y}{0.08 x - 0.5 y} = \frac{3 x - 20 y}{8 x - 50 y}$ D、 $- \frac{x^{2} - x + 2}{3 x^{2} - 5 x^{3} - 2} = - \frac{x^{2} - x + 2}{5 x^{3} - 3 x^{2} + 2}$

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 15 °$ ， $D E$ 垂直平分 $A B$ ，交 $B C$ 于点 $E$ ， $B E = 10 c m$ ，则边 $A C$ 的长为（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
5. 如图，已知△ABC是等边三角形，点B、C，D、E在同一直线上，且CG=CD，DF=DE，则∠E=（）

A、30° B、25° C、15° D、10°

查看试题解析
6. 若 $a^{2} - a b = 0$ （b≠0），则 $\frac{a}{a + b}$ =（）

A、0 B、 $\frac{1}{2}$ C、0或 $\frac{1}{2}$ D、1或 2

查看试题解析
7. 某班学生周末乘汽车到外地参加活动，目的地距学校 $120 k m$ ，一部分学生乘慢车先行，出发 $1 h$ 后，另一部分学生乘快车前往，结果他们同时到达目的地，已知快车速度是慢车速度的2倍，如果设慢车的速度为 $x k m / h$ ，那么可列方程为（）

A、 $\frac{120}{x} - \frac{120}{2 x} = 1$ B、 $\frac{120}{x} - \frac{120}{2 + x} = 1$ C、 $\frac{120}{2 x} - \frac{120}{x} = 1$ D、 $\frac{120}{x + 2} - \frac{120}{x} = 1$

查看试题解析
8. 若方程 $\frac{3 - 2 x}{x - 3} + \frac{2 + m x}{3 - x} = - 1$ 无解，则 $m$ 的值为（）

A、-1 B、-1或 $- \frac{5}{3}$ C、3 D、-1或3

查看试题解析
9. 如图，在等腰△ABC中，AB＝AC，∠A＝20°，AB上一点D，且AD＝BC，过点D作DE∥BC且DE＝AB，连接EC，则∠DCE的度数为（）

A、80° B、70° C、60° D、45°

查看试题解析
10. 如图，已知AB＝AC，AF＝AE，∠EAF＝∠BAC，点C、D、E、F共线．则
下列结论，其中正确的是（）

①△AFB≌△AEC；②BF＝CE；③∠BFC＝∠EAF；④AB＝BC．

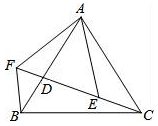A、①②③ B、①②④ C、①② D、①②③④

查看试题解析

二、填空题

11. 科学家测得肥皂泡的厚度约为0.000 000 7米，0.000 000 7用科学记数法表示为．

查看试题解析
12. 若分式 $\frac{2 - | x |}{x + 2}$ 的值为零，则x的值为.

查看试题解析
13. 已知 $4 x^{2} + k x y + 9 y^{2}$ 是一个完全平方式，则 $k$ 的值是．

查看试题解析
14. 若 ${(x + y)}^{2} = 9$ ， ${(x - y)}^{2} = 5$ ，则 $x y$ =

查看试题解析
15. 已知： ${(\frac{27}{8})}^{x - 1} • {(\frac{2}{3})}^{2 x - 3} = \frac{4}{9}$ ，则 $x =$

查看试题解析
16. 如图，在 $△ A B C$ 中， $B C$ 的垂直平分线 $E F$ 交 $∠ A B C$ 的平分线 $B D$ 于 $E$ ，若 $∠ B A C = 60 °$ ， $∠ A C E = 24 °$ ，则 $∠ B E F$ 的度数是．

查看试题解析
17. 如图，已知正六边形ABCDEF的边长是5，点P是AD上的一动点，则PE＋PF的最小值是.

查看试题解析
18. 若 ${(1 - x)}^{1 - 3 x} = 1$ ，则 $x$ 可取的值为．

查看试题解析
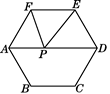19. 在△ABC中， AB=AC，∠BAC=100°，点D在BC边上，连接AD，若△ABD为直角三角形，则∠ADC的度数为.

查看试题解析
20. 我国南宋数学家杨辉所著的《详解九章算术》一书上，用如图的三角形解释二项式 ${(a + b)}^{n}$ 的展开式的各项系数，此三角形称为“杨辉三角”，根据“杨辉三角”，请计算 ${(a + b)}^{8}$ 的展开式中从左起第三项的系数为．

查看试题解析

三、解答题

21.

(1)、计算： ${(2019 - π)}^{0} + {(- \frac{1}{3})}^{- 2}$

(2)、计算： $(x - 2 y) (x^{2} - 4 y^{2}) (x + 2 y)$

(3)、因式分解： $3 a x^{2} - 6 a x y + 3 a y^{2}$

(4)、解方程： $\frac{2 + x}{2 - x} + \frac{16}{x^{2} - 4} = - 1$

查看试题解析
22. 先化简，再求值： $(\frac{x^{2}}{x - 1} - x + 1) \div \frac{4 x^{2} - 4 x + 1}{1 - x}$ ，其中 $x = 2$ ．．

查看试题解析
23.
如图，△ABC和△DAE中，∠BAC=∠DAE，AB=AE，AC=AD，连接BD，CE，

求证：△ABD≌△AEC．

查看试题解析
24. $△ A B C$ 是等边三角形，作直线 $A P$ ，点 $C$ 关于直线 $A P$ 的对称点为 $D$ ，连接 $A D$ ，直线 $B D$ 交直线 $A P$ 于点 $E$ ，连接 $C E$ ．

(1)、如图①，求证： $C E + A E = B E$ ；（提示：在BE上截取 $B F = D E$ ，连接 $A F$ ．）

(2)、如图②、图③，请直接写出线段 $C E$ ， $A E$ ， $B E$ 之间的数量关系，不需要证明；

(3)、在（1）、（2）的条件下，若 $B D = 2 A E = 6$ ，则 $C E =$ ．

查看试题解析
25. 为庆祝中华人民共和国七十周年华诞，某校举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生已知用300元购买甲种文具的个数是用50元购买乙种文具个数的2倍，购买1个甲种文具比购买1个乙种文具多花费10元．

(1)、求购买一个甲种文具、一个乙种文具各需多少元；

(2)、若学校计划购买这两种文具共120个，投入资金不多于1000元，且甲种文具至少购买36个，求有多少种购买方案．

查看试题解析
26. 如图，在平面直角坐标系中，点 $A$ ， $B$ 分别在 $y$ 轴， $x$ 轴正半轴上．

(1)、 $∠ O A B$ 的平分线与 $∠ A B O$ 的外角平分线交于点 $C$ ，求 $∠ C$ 的度数；

(2)、设点 $A$ ， $B$ 的坐标分别为 $(0 ， a)$ ， $(b ， 0)$ ，且满足 $a^{2} - 4 a + b^{2} - 2 b + 5 = 0$ ，求 $S_{△ O A B}$ 的面积；

(3)、在（2）的条件下，当 $△ A B D$ 是以 $A B$ 为斜边的等腰直角三角形时，请直接写出点 $D$ 的坐标．

查看试题解析