黑龙江省哈尔滨市松北区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、（2x⁵）²=2x¹⁰ B、（﹣3）^﹣2= $\frac{1}{9}$ C、（a+1）²=a²+1 D、a²•a³=a⁶

查看试题解析
2. 下列四个图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列长度的四根木棒中，能与 $4 c m ， 9 c m$ 长的两根木棒首尾相接成一个三角形的是（）

A、 $4 c m$ B、 $5 c m$ C、 $9 c m$ D、 $13 c m$

查看试题解析
4. 人体中红细胞的直径约为0.0000077 m，用科学记数法表示数的结果是（）

A、0.77×10^－⁵ m B、0.77×10^－⁶ m C、7.7×10^－⁵ m D、7.7×10^－⁶ m

查看试题解析
5. 下列二次根式中的最简二次根式是（）

A、 $\sqrt{30}$ B、 $\sqrt{12}$ C、 $\sqrt{8}$ D、 $\sqrt{0.5}$

查看试题解析
6. 计算12a²b⁴•(﹣ $\frac{3 a}{2 b^{3}}$ )÷(﹣ $\frac{a^{2} b}{2}$ )的结果等于（）

A、﹣9a B、9a C、﹣36a D、36a

查看试题解析
7. 已知图中的两个三角形全等，则∠α的度数是（）

A、72° B、60° C、58° D、50°

查看试题解析
8. 计算： $\sqrt{{(2 a - 1)}^{2}} + \sqrt{{(1 - 2 a)}^{2}}$ 的值是（）

A、0 B、 $4 a - 2$ C、 $2 - 4 a$ D、 $2 - 4 a$ 或 $4 a - 2$

查看试题解析
9. 如果 $x^{2} + (m - 2) x + 9$ 是个完全平方式，那么 $m$ 的值是（）

A、8 B、-4 C、±8 D、8或-4

查看试题解析
10. 如图，MN是等边三角形ABC的一条对称轴，D为AC的中点，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD的度数是（）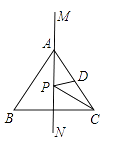

A、30° B、15° C、20° D、35°

查看试题解析

二、填空题

11. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为零，则x的值为．

查看试题解析
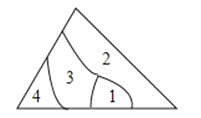
12. 若把多项式x²+5x﹣6分解因式为．

查看试题解析
13.
小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形？应该带第块．

查看试题解析
14. 如图，△ABC中，∠BAC＝70°，∠ABC的平分线与∠ACB的外角平分线交于点O，则∠BOC＝度．

查看试题解析
15. 若多项式9x²﹣2（m+1）xy+4y²是一个完全平方式，则m＝.

查看试题解析
16. 若m+n=3，则代数式m²+2mn+n²－6的值为．

查看试题解析
17. 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF＝AC，则∠ABC＝度．

查看试题解析
18. 若最简二次根式 $\sqrt[a + 3]{2 a + 5}$ 与 $\sqrt{3 b + 4 a}$ 是同类二次根式，则a＝．

查看试题解析
19. 在平面直角坐标系xOy中，已知点A（2，3），在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有个．

查看试题解析
20. 如图，在 $R t Δ A B C$ 中， $∠ A B C = 90 °$ ， $A B = 6$ ， $B C = 8$ ， $∠ B A C$ ， $∠ A C B$ 的平分线相交于点E，过点E作 $E F / / B C$ 交AC于点F，则 $E F =$ ；

查看试题解析

三、解答题

21. 化简求值： $\frac{3}{x^{2} - 4 x + 4} \div \frac{2 x + 4}{x^{2} - 4} - \frac{1}{x - 2}$ ，其中，x＝2+ $\sqrt{2}$ ．

查看试题解析
22. 如图，已知A（0，4）、B（﹣2，2）、C（3，0）．

(1)、作△ABC关于x轴对称的△A₁B₁C₁ ，并写出点B的对应点B₁的坐标；

(2)、求△A₁B₁C₁的面积S．

查看试题解析
23. 已知a，b分别为等腰三角形的两条边长，且a，b满足b＝4＋ $\sqrt{3 a - 6}$ ＋3 $\sqrt{2 - a}$ ，求此三角形的周长.

查看试题解析
24. 如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小矩形，且m＞n．（以上长度单位：cm）

(1)、观察图形，可以发现代数式2m²+5mn+2n²可以因式分解为；

(2)、若每块小矩形的面积为10cm² ，两个大正方形和两个小正方形的面积和为58cm² ，试求m+n的值

(3)、②图中所有裁剪线（虚线部分）长之和为 cm．（直接写出结果）

查看试题解析
25. 某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求．商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．

(1)、该商家购进的第一批衬衫是多少件？

(2)、若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润率不低于25%（不考虑其它因素），那么每件衬衫的标价至少是多少元？

查看试题解析
26. 已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．

(1)、如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．
①求证：∠1＝∠2；

②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；

(2)、如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求 $\frac{S_{△ A B F}}{S_{△ A C F}}$ 的值．

查看试题解析
27. 已知：平面直角坐标系中，点A（a，b）的坐标满足|a﹣b|+b²﹣8b+16＝0.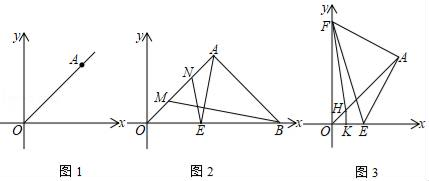

(1)、如图1，求证：OA是第一象限的角平分线；

(2)、如图2，过A作OA的垂线，交x轴正半轴于点B，点M、N分别从O、A两点同时出发，在线段OA上以相同的速度相向运动（不包括点O和点A），过A作AE⊥BM交x轴于点E，连BM、NE，猜想∠ONE与∠NEA之间有何确定的数量关系，并证明你的猜想；

(3)、如图3，F是y轴正半轴上一个动点，连接FA，过点A作AE⊥AF交x轴正半轴于点E，连接EF，过点F点作∠OFE的角平分线交OA于点H，过点H作HK⊥x轴于点K，求2HK+EF的值.

查看试题解析