黑龙江省哈尔滨市南岗区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-10-29 类型:期末考试
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列四个式子中是分式的是( )A、 B、 C、 D、3. 下列计算中正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点 关于 轴的对称点坐标为( )A、 B、 C、 D、5. 计算22+(-1)0的结果是( ).
2. 下列四个式子中是分式的是( )A、 B、 C、 D、3. 下列计算中正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点 关于 轴的对称点坐标为( )A、 B、 C、 D、5. 计算22+(-1)0的结果是( ).
A、5 B、4 C、3 D、26. 式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、7. 下列变形中是因式分解的是( )A、 B、 C、 D、8. 计算: 的结果是( )A、 B、 C、 D、9. 下列四个分式方程中无解的是( ).A、 B、 C、 D、10. 若2m=a,32n=b,m,n均为正整数,则23m+10n的值为( )A、a b B、a b C、a +b D、a b二、填空题
-
11. 世界科技不断发展,人们制造出的晶体管长度越来越短,某公司研发出长度只有0.000000006米的晶体管,该数用科学记数法表示为米.12. 若分式 的值为0,则 的值为.13. 计算( )( )的结果等于 .
14. 若分式 有意义,则 的取值范围是 .15. 把多项式 分解因式的结果是 .16. 计算 的结果是17. 在 中, ,若 ,则 度18. 计算: .19. 已知a+ = ,则a- =20. 如图,在 中, , ,过点 作 ,连接 ,过点 作 于点 ,若 , 的面积为6,则 的长为 .
三、解答题
-
21. 计算:(1)、(2)、22. 计算:(1)、(2)、23. 先化简,再求代数式 的值,其中24. 已知a,b分别是6- 的整数部分和小数部分.(1)、求a,b的值;(2)、求3a-b2的值.25. 甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的1.5倍,两人各加工600个这种零件,甲比乙少用5天.(1)、甲、乙两人每天各加工多少个这种零件?(2)、已知甲、乙两人加工这种零件每天的加工费分别是150元和120,现有1600个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过4200元,那么甲至少加工了多少天?26. 已知:在 中, ,点 在 上,连结 ,且 .(1)、如图1,求 的度数;
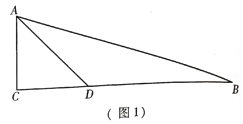 (2)、如图2, 点 在 的垂直平分线上,连接 ,过点 作 于点 , 交 于点 ,若 , ,求证: 是等腰直角三角形;
(2)、如图2, 点 在 的垂直平分线上,连接 ,过点 作 于点 , 交 于点 ,若 , ,求证: 是等腰直角三角形; (3)、如图3,在(2)的条件下,连接 ,过点 作 交 于点 ,且 ,若 ,求 的长.
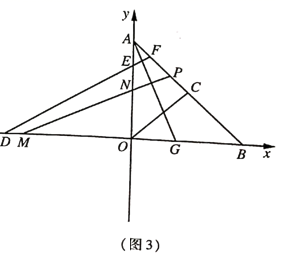
(3)、如图3,在(2)的条件下,连接 ,过点 作 交 于点 ,且 ,若 ,求 的长. 27. 已知:在平面直角坐标系中,点 为坐标原点, 的顶点 的坐标为 ,顶点 在 轴上(点 在点 的右侧),点 在 上,连接 ,且 .(1)、如图1,求点 的纵坐标;
27. 已知:在平面直角坐标系中,点 为坐标原点, 的顶点 的坐标为 ,顶点 在 轴上(点 在点 的右侧),点 在 上,连接 ,且 .(1)、如图1,求点 的纵坐标;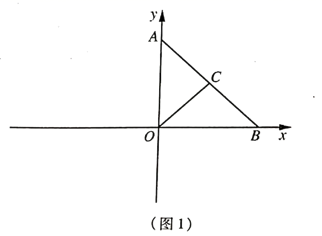 (2)、如图2,点 在 轴上(点 在点 的左侧),点 在 上,连接 交 于点 ;若 ,求证:
(2)、如图2,点 在 轴上(点 在点 的左侧),点 在 上,连接 交 于点 ;若 ,求证: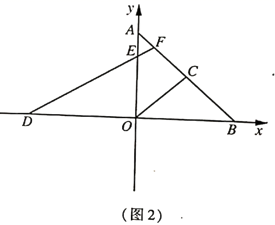 (3)、如图3,在(2)的条件下, 是 的角平分线,点 与点 关于 轴对称,过点 作 分别交 于点 ,若 ,求点 的坐标.
(3)、如图3,在(2)的条件下, 是 的角平分线,点 与点 关于 轴对称,过点 作 分别交 于点 ,若 ,求点 的坐标.