黑龙江省哈尔滨市宾县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-29 类型：期末考试

进入出卷网下载

一、单选题

1. 在代数式 $\frac{2}{3} x ， \frac{1}{x} ， \frac{2}{3} x y^{2} ， \frac{3}{x + 4} ， \frac{2 x^{2} + 5}{2 x} ， x^{2} - \frac{2}{3}$ 中，分式共有（）．

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列线段长能构成三角形的是（）

A、3、4、7 B、2、3、6 C、5、6、11 D、4、7、10

查看试题解析
3. 等腰三角形两边长分别为4和8，则这个等腰三角形的周长为( )

A、16 B、18 C、20 D、16或20

查看试题解析
4. 点(2，-3)关于y轴的对称点是（）

A、 $(- 2 ， 3)$ B、 $(2 ， 3)$ C、 $(- 2 ， - 3)$ D、 $(2 ， - 3)$

查看试题解析
5. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列命题中错误的是（）

A、全等三角形的对应边相等 B、全等三角形的面积相等 C、全等三角形的周长相等 D、周长相等的两个三角形全等

查看试题解析
7. 如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（）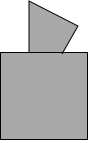

A、SSS B、SAS C、AAS D、ASA

查看试题解析
8. 下列计算正确的是（）

A、3x﹣2x＝1 B、a﹣（b﹣c+d）＝a+b+c﹣d C、（﹣a²）²＝﹣a⁴ D、﹣x•x²•x⁴＝﹣x⁷

查看试题解析
9. 若 $3^{x} {=4, 9}^{y} =7$ ，则 $3^{x - 2y}$ 的值为（）

A、 $\frac{4}{7}$ B、 $\frac{7}{4}$ C、-3 D、 $\frac{2}{7}$

查看试题解析
10. 已知关于x的分式方程 $\frac{m}{x - 1}$ + $\frac{3}{1 - x}$ =1的解是非负数，则m的取值范围是（）

A、m＞2 B、m≥2 C、m≥2且m≠3 D、m＞2且m≠3

查看试题解析

二、填空题

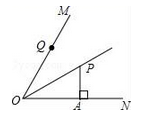
11. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为.

查看试题解析
12. 一个多边形的各内角都相等，且每个内角与相邻外角的差为100°，那么这个多边形的边数是.

查看试题解析
13. 如图， OP平分 $∠ M O N$ ， $P A ⊥ O N$ 于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为．

查看试题解析
14. x+ $\frac{1}{x}$ ＝3，则x²+ $\frac{1}{x^{2}}$ ＝．

查看试题解析
15.
如图，从镜子中看到一钟表的时针和分针，此时的实际时刻是．

查看试题解析
16. 分解因式：（x²+4）²﹣16x²＝．

查看试题解析
17. （ $\frac{3}{4}$ x²y﹣ $\frac{1}{3}$ xy² $+ \frac{1}{2} x y$ ）÷ $\frac{1}{12}$ xy＝．

查看试题解析
18. 三角形有两条边的长度分别是5和7，则最长边a的取值范围是．

查看试题解析
19. 已知△ABC中，AB=AC，AB的垂直平分线交AB于点D，交直线AC于点E.若∠EBC=42°，则∠BAC的度数为

查看试题解析
20. 一个六边形的六个内角都是120°，连续四边的长依次为2.31，2.32，2.33，2.31，则这个六边形的周长为．

查看试题解析

三、解答题

21. 计算：

(1)、（﹣3a²b）³﹣（2a³）²•（﹣b）³+3a⁶b³

(2)、（2a+b）（2a﹣b）﹣（a﹣b）²

查看试题解析
22. 如图，已知在平面直角坐标系中，△ABC三个顶点的坐标分别是A(1，1)，B (4，2)，C(3，4)．

(1)、画出△ABC关于y轴对称的△A₁B₁C₁（要求：A与A₁ ， B与B₁ ， C与C₁相对应）；

(2)、通过画图，在x轴上确定点Q，使得QA与QB之和最小，画出QA与QB，并直接写出点Q的坐标．点Q的坐标为．

查看试题解析
23. 先化简，再求值： $\frac{x^{2} + 2 x + 1}{x + 2}$ ÷ $\frac{x^{2} - 1}{x - 1}$ ﹣ $\frac{x}{x + 2}$ ，其中x＝（5﹣π）⁰+（﹣2）^﹣¹ ．

查看试题解析
24. 如图，AE＝AD，∠ABE＝∠ACD，BE与CD相交于O．

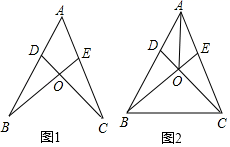(1)、如图1，求证：AB＝AC；

(2)、如图2，连接BC、AO，请直接写出图2中所有的全等三角形（除△ABE≌△ACD外）．

查看试题解析
25. 京沈高速铁路赤峰至喀左段正在建设中，甲、乙两个工程队计划参与一项工程建设，甲队单独施工30天完成该项工程的 $\frac{1}{3}$ ，这时乙队加入，两队还需同时施工15天，才能完成该项工程．

(1)、若乙队单独施工，需要多少天才能完成该项工程?

(2)、若甲队参与该项工程施工的时间不超过36天，则乙队至少施工多少天才能完成该项工程?

查看试题解析
26. 如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”．

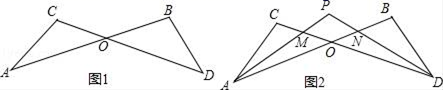(1)、求证：∠A+∠C＝∠B+D；

(2)、如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD、AB分别相交于点M、N．在图1中，有∠A+∠C＝180°﹣∠AOC，∠B+∠D＝180°﹣∠BOD，
∵∠AOC＝∠BOD，

∴∠A+∠C＝∠B+∠D；

以线段AC为边的“8字型”有个，以点O为交点的“8字型”有个；

(3)、①若∠B＝100°，∠C＝120°，求∠P的度数；
②若角平分线中角的关系改为“∠CAP＝ $\frac{1}{3}$ ∠CAB，∠CDP＝ $\frac{1}{3}$ ∠CDB”，试探究∠P与∠B、∠C之间存在的数量关系，并证明理由．

查看试题解析
27. 在△ABC中，AB＝AC，D、E分别在BC和AC上，AD与BE相交于点F．

(1)、如图1，若∠BAC＝60°，BD＝CE，求证：∠1＝∠2；

(2)、如图2，在（1）的条件下，连接CF，若CF⊥BF，求证：BF＝2AF；

(3)、如图3，∠BAC＝∠BFD＝2∠CFD＝90°，若S_△_ABC＝2，求S_△_CDF的值．

查看试题解析