黑龙江省大庆市龙凤区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-10-29 类型:期末考试
一、单选题
-
1. 下列分解因式正确的是A、 B、 C、 D、2. 下列四个分式中,是最简分式的是( )A、 B、 C、 D、3. 若多项式 能用完全平方公式进行因式分解,则 值为( )A、2 B、-2 C、±2 D、±44. 如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
 A、2cm B、3cm C、4cm D、5cm5. 计算 ,得( )A、 B、 C、 D、6. 如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )
A、2cm B、3cm C、4cm D、5cm5. 计算 ,得( )A、 B、 C、 D、6. 如图所示,线段AC的垂直平分线交线段AB于点D,∠A=50°,则∠BDC=( )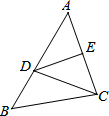 A、50° B、100° C、120° D、130°7. 分式 中的x、y同时扩大2倍,则分式值( )A、不变 B、是原来的2倍 C、是原来的4倍 D、是原来的8. 若不等式组 ,只有三个正整数解,则a的取值范围为( )A、0≤a<1 B、0<a<1 C、0<a≤1 D、0≤a≤19. 两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地,设第二组的步行速度为x千米/小时,根据题意可列方程是( ).A、 B、 C、 D、10.
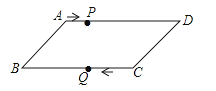
A、50° B、100° C、120° D、130°7. 分式 中的x、y同时扩大2倍,则分式值( )A、不变 B、是原来的2倍 C、是原来的4倍 D、是原来的8. 若不等式组 ,只有三个正整数解,则a的取值范围为( )A、0≤a<1 B、0<a<1 C、0<a≤1 D、0≤a≤19. 两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地,设第二组的步行速度为x千米/小时,根据题意可列方程是( ).A、 B、 C、 D、10.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
 A、4次 B、3次 C、2次 D、1次
A、4次 B、3次 C、2次 D、1次二、填空题
-
11. 若已知 , ,则x-y= .12. 函数 中自变量x的取值范围是.13. 若正多边形的每一个内角为 ,则这个正多边形的边数是 .14.
如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
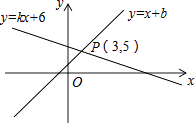 15. 已知m=2n+1,则m2﹣4mn+4n2﹣5的值为 .16. 已知关于x的方程 无解,则 .17. 如图,等腰三角形ABC的底边BC的长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F , 若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .
15. 已知m=2n+1,则m2﹣4mn+4n2﹣5的值为 .16. 已知关于x的方程 无解,则 .17. 如图,等腰三角形ABC的底边BC的长为4,面积是12,腰AB的垂直平分线EF分别交AB、AC于点E、F , 若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 .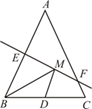 18. 如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG , 点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为 .
18. 如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG , 点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为 .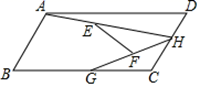
三、解答题
-
19. 因式分解(1)、 ;(2)、 .20. 解分式方程:21. 解不等式组: ;并将解集在数轴上表示出来.
 22. 先化简再求值: ,再从0,-1,2中选一个数作为 的值代入求值.23. 如图,在▱ABCD中,E、F分别是BC、AD边上的点,且∠1=∠2.求证:四边形AECF是平行四边形.
22. 先化简再求值: ,再从0,-1,2中选一个数作为 的值代入求值.23. 如图,在▱ABCD中,E、F分别是BC、AD边上的点,且∠1=∠2.求证:四边形AECF是平行四边形. 24. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
24. 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形). (1)、将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;(3)、直接写出点B2 , C2的坐标.25. 某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)、将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;(2)、将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;(3)、直接写出点B2 , C2的坐标.25. 某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)、甲、乙两种书柜每个的价格分别是多少元?
(2)、若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
26. 如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.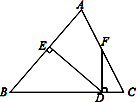 (1)、若∠AFD=155°,求∠EDF的度数;(2)、若点F是AC的中点,求证:∠CFD= ∠B.27. 甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.(1)、求甲、乙两个工程队每天各修路多少千米?(2)、若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?28. 基本图形:在RT△ABC中,AB=AC , D为BC边上一点(不与点B , C重合),将线段AD绕点A逆时针旋转90°得到AE .
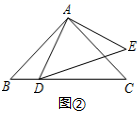
(1)、若∠AFD=155°,求∠EDF的度数;(2)、若点F是AC的中点,求证:∠CFD= ∠B.27. 甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.(1)、求甲、乙两个工程队每天各修路多少千米?(2)、若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?28. 基本图形:在RT△ABC中,AB=AC , D为BC边上一点(不与点B , C重合),将线段AD绕点A逆时针旋转90°得到AE .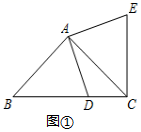
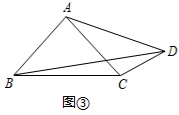
探索:
(1)、连接EC , 如图①,试探索线段BC , CD , CE之间满足的等量关系,并证明结论;(2)、连接DE , 如图②,试探索线段DE , BD , CD之间满足的等量关系,并证明结论;(3)、联想:如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=7,CD=2,则AD的长为 .