初中数学苏科版七年级上册4.2解一元一次方程同步练习

试卷更新日期：2020-10-29 类型：同步测试

进入出卷网下载

一、单选题

1. 下列说法中，正确的是（　　）

A、方程是等式 B、等式是方程 C、含有字母的等式是方程 D、不含字母的方程是等式

查看试题解析
2. 如果关于x的方程3x+2k-5=0的解为x=-3，则k的值是（）

A、2 B、-2 C、7 D、-7

查看试题解析
3. 下列等式变形正确的是（）

A、若﹣2x＝5，则x＝ $- \frac{2}{5}$ B、若3（x+1）﹣2x＝1，则3x+1﹣2x＝1 C、若5x﹣6＝﹣2x﹣8，则5x+2x＝8+6 D、若 $\frac{x}{3} + \frac{x - 1}{2} = 1$ ，则2x+3（x﹣1）＝6

查看试题解析
4. 若关于x的方程2k﹣3x=4与x﹣2=0的解相同，则k的值为（　　）

A、﹣10 B、10 C、﹣5 D、5

查看试题解析
5. 若2m +3与-13互为相反数，则 m 的值是（）

A、-2 B、2 C、-5 D、5

查看试题解析
6. 若关于x的方程3(x＋k)＝x＋6的解是非负数，则k的取值范围是（）

A、k≥2 B、k＞2 C、k≤2 D、k＜2

查看试题解析
7. 方程 $2 - \frac{3 x - 7}{4} = - \frac{x + 17}{5}$ 去分母得（）

A、2-5（3x-7）=-4（x+17） B、40-15x-35=-4x-68 C、40-5（3x-7）=-4x+68 D、40-5（3x-7）=-4（x+17）

查看试题解析
8. 方程 $| 2 x + 1 | = 5$ 的解是（）

A、2 B、﹣3 C、 $\pm 2$ D、2或﹣3

查看试题解析
9. 小马虎做作业时，不小心将方程中的一个常数污染了，被污染的方程是2（x－3）－■＝x＋1，怎么办呢？他想了想，便翻看书后的答案，方程的解是x＝9，请问这个被污染的常数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
10. 解方程的过程中正确的是（）．

A、将2- 去分母，得2-5（5x-7）=-4（x+17） B、由 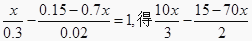=100 C、40-5（3x-7）=2（8x+2）去括号，得40-15x-7=16x+4 D、- x=5，得x=-

查看试题解析

二、填空题

11. 若关于x的方程2x-m=x-2的解是3，则m的值为。

查看试题解析
12. 若代数式2x﹣1与x+2的值相等，则x＝．

查看试题解析
13. 关于 $x$ 的方程 $2 x - 4 = 3 m$ 和 $x + 2 = 1$ 有相同的解，那么m＝．

查看试题解析
14. 规定一种运算“*”，a*b= $\frac{1}{3}$ a﹣ $\frac{1}{4}$ b，则方程x*2=1*x的解为．

查看试题解析
15. 已知方程（a-2）x^|a|-1=1是一元一次方程，则a= ， x= ．

查看试题解析
16. 已知a ， b为定值，关于x的方程 $\frac{k x + a}{3} = 1 - \frac{2 x + b k}{6}$ ，无论k为何值，它的解总是1，则a+b＝．

查看试题解析
17. 小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是：2y－ $\frac{1}{2}$ ＝ $\frac{1}{2}$ y－，怎么办呢？小明想了一想，便翻看书后答案，此方程的解是y＝－ $\frac{5}{3}$ ，于是很快就补好了这个常数，你能补出这个常数吗？它应是．

查看试题解析
18. 规定：用 ${m}$ 表示大于 $m$ 的最小整数，例如 ${\frac{5}{2}} = 3$ ， ${4} = 5$ ， ${- 1.5} = - 1$ 等；用 $[m]$ 表示不大于 $m$ 的最大整数，例如 $[\frac{7}{2}] = 3$ ， $[2] = 2$ ， $[- 3.2] = - 4$ ，如果整数 $x$ 满足关系式： $2 {x} + 3 [x] = 32$ ，则 $x =$ .

查看试题解析

三、解答题

19. 解方程

(1)、5x+3=﹣7x+9

(2)、5（x﹣1）﹣2（3x﹣1）=4x﹣1

(3)、 $\frac{3 x + 1}{2}$ = $\frac{7 + x}{6}$

(4)、 $\frac{x}{2}$ ﹣ $\frac{5 x + 11}{6}$ =1+ $\frac{2 x - 4}{3}$

(5)、 $\frac{3 + 0.2 x}{0.2}$ ﹣ $\frac{0.2 + 0.03 x}{0.01}$ =0.75．

查看试题解析
20. 列方程求解

(1)、m为何值时，关于x的一元一次方程4x﹣2m=3x﹣1的解是x=2x﹣3m的解的2倍．

(2)、已知|a﹣3|+（b+1）²=0，代数式 $\frac{2 b - a + m}{2}$ 的值比 $\frac{1}{2}$ b﹣a+m多1，求m的值．

查看试题解析
21. 定义新运算：对于任意有理数a，b，都有a⊗b=a（a﹣b）+1，等式右边是通常的加法、减法及乘法运算，比如：2⊗5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5

(1)、求（﹣2）⊗3的值；

(2)、若4⊗x的值等于13，求x的值．

查看试题解析
22. 如果关于 $x$ 的方程 $\frac{2 x - 3}{5} = \frac{2}{3} x - 3$ 与 $3 n - 1 = 3 (x + n) - 2 n$ 的解相同，求 $n$ 的值.

查看试题解析
23. 在作解方程练习时，学习卷中有一个方程“ $2 y - \frac{1}{3} = \frac{1}{3} y + □$ ”中的 $□$ 没印清晰，小聪问老师，老师只是说：“ $□$ 是个有理数，该方程的解与方程 $3 (x - 1) - 2 (x - 2) = 3$ 的解相同.”小聪很快补上了这个常数，聪明的你能补上这个常数吗？

查看试题解析
24. 阅读下面的解题过程：
解方程：|x+3|=2．
解：当x+3≥0时，原方程可化成为x+3=2
解得x=﹣1，经检验x=﹣1是方程的解；
当x+3＜0，原方程可化为，﹣（x+3）=2
解得x=﹣5，经检验x=﹣5是方程的解．
所以原方程的解是x=﹣1，x=﹣5．
解答下面的两个问题：
（1）解方程：|3x﹣2|﹣4=0；
（2）探究：当值a为何值时，方程|x﹣2|=a，
①无解；②只有一个解；③有两个解．

查看试题解析

初中数学苏科版七年级上册4.2解一元一次方程 同步练习

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级上册4.2解一元一次方程同步练习